Aula 19: Funções Recursivas

Tópicos

• fatorial recursivo.
• cálculo da série de Fibonacci.
• função recursiva para cálculo de potência.
• exemplo de listas com recursão.
• Torre de Hanoi.

Uma função é dita recursiva quando dentro dela é feita uma ou mais chamadas a ela mesma.

A ideia é dividir um problema original um subproblemas menores de mesma natureza (divisão) e depois combinar as soluções obtidas para gerar a solução do problema original de tamanho maior (conquista). Os subproblemas são resolvidos recursivamente do mesmo modo em função de instâncias menores, até se tornarem problemas triviais que são resolvidos de forma direta, interrompendo a recursão.

Exemplo 1:

Solução 1:

Solução não recursiva.

def fatorial(n):
 fat = 1
 while n > 1:
    fat *= n
    n -= 1
 return fat
  

Solução 2:

Solução recursiva: n! = n.(n-1)!

def fatorial(n):
  if n == 0: #Caso trivial
    return 1 #Solução direta
  else:
    return n*fatorial(n-1) #Chamada recursiva
  

Problema 1: Cálculo da série de Fibonacci

Exemplo da sequência:

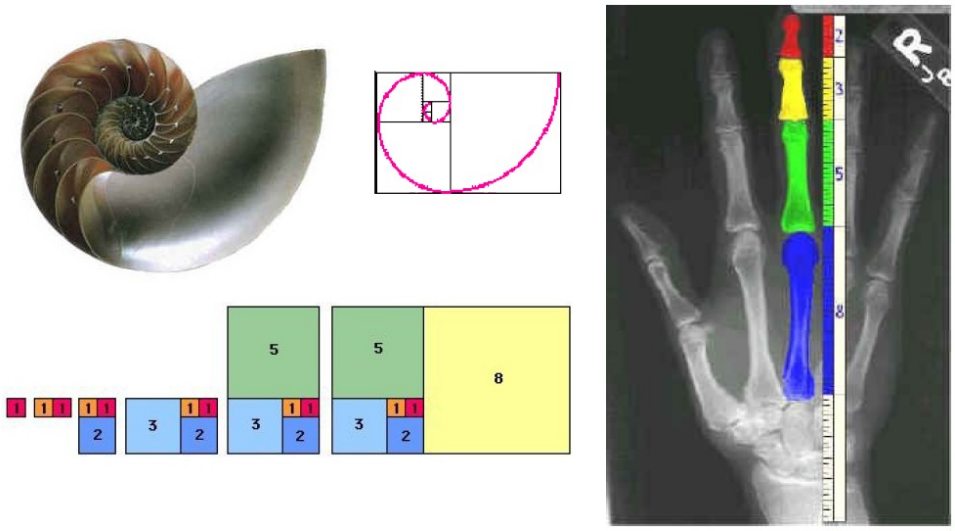
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

Solução 1:

Versão recursiva:

def fibo(n):
  if n <= 1:
    return n
  else:
    return fibo(n-1) + fibo(n-2)
  

Solução 2:

Versão não recursiva:

def fibo(n):
  f0 = 0
  f1 = 1
  for k in range(1,n+1):
    f2 = f0 + f1
    f0 = f1
    f1 = f2
  return f0
  

Neste caso não faz sentido utilizar a versão recursiva.

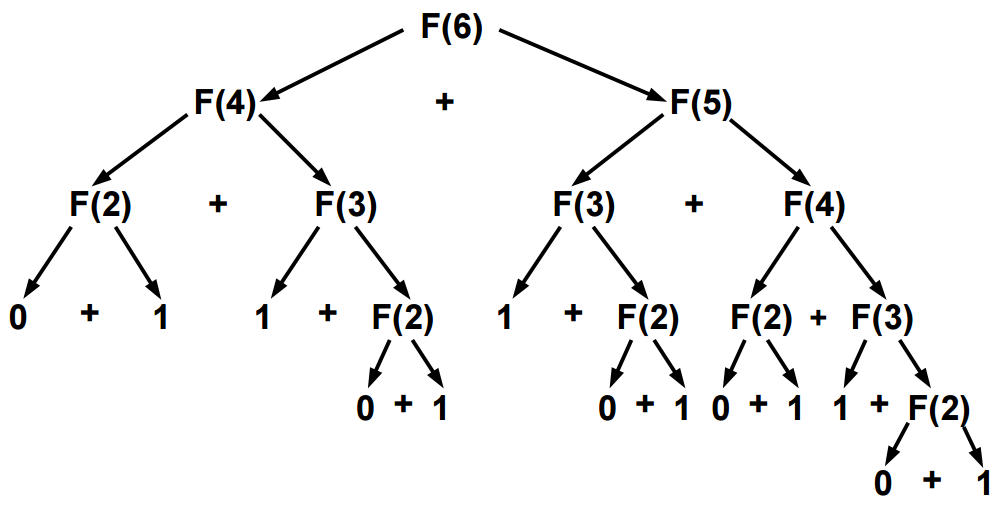
Árvore de Recorrência:

A solução recursiva é ineficiente, pois recalcula várias vezes a solução para valores intermediários:

Por exemplo, para F(6)=fibo(6) = 8, temos 2xF(4), 3xF(3), 5xF(2).

Problema 2:

Solução 1:

Solução não recursiva.

def potencia(x, n):
  pot = 1.0
  while n > 0:
    pot *= x
    n -= 1
  return pot
  

Solução 2:

Solução recursiva: x^n = x . x^(n-1)

def potencia(x, n):
  if n == 0:    #Caso trivial
    return 1.0  #Solução direta
  else:
    return x*potencia(x, n-1) #Chamada recursiva
  

Solução 3:

Solução recursiva: x^n = x^(n/2). x^(n/2) = (x^(n/2))^2

def potencia(x, n):
  if n == 0: #Caso trivial
    return 1.0 
  elif n%2 == 0: #Se n é par...
    pot = potencia(x, n//2)
    return pot*pot
  else: #Se n é ímpar...
    pot = potencia(x, n//2)
    return pot*pot*x
  

Problema 3:

Solução 1:

Realiza a chamada recursiva em uma cópia de um subtrecho da lista com um elemento a menos, após fatiamento que não copia o último elemento.

def maiorValor(L):
  if len(L) == 1:
    return L[0]
  else:
    m = maiorValor(L[:len(L)-1])
    if m > L[len(L)-1]:
      return m
    else:
      return L[len(L)-1]
  

Solução 2:

Realiza a chamada recursiva em uma cópia de um subtrecho da lista com um elemento a menos, após fatiamento que não copia o primeiro elemento.

def maiorValor(L):
  if len(L) == 1:
    return L[0]
  else:
    m = maiorValor(L[1:])
    if m > L[0]:
      return m
    else:
      return L[0]
  

Solução 3:

Realiza a chamada recursiva no subtrecho da lista com um elemento a menos, após a remoção do seu último elemento via o método pop(). Este último elemento é então posteriormente reposto na lista a fim de preservar o seu conteúdo original, através do método append().

def maiorValor(L):
  if len(L) == 1:
    return L[0]
  else:
    ult = L.pop()
    m = maiorValor(L)
    L.append(ult)
    if m > ult:
      return m
    else:
      return ult
  

Solução 4:

Evita o uso de fatiamento de listas e de remoções, usando uma segunda função auxiliar maiorValorAux(L,n) com um parâmetro extra para realizar a recursão. A função maiorValor(L) passa a ser apenas uma função de embrulho (wrapper function).

#Encontra o maior valor de uma lista com n elementos.
def maiorValorAux(L, n):
  if n==1: #Caso trivial
    return L[0]
  else:
    m = maiorValorAux(L, n-1)
    if m > L[n-1]:
      return m
    else:
      return L[n-1]


def maiorValor(L):
  n = len(L)
  return maiorValorAux(L, n)
  

Problema 4:

Solução 1:

def inverte(L):
    n = len(L)
    if n > 1:
        T = inverte(L[:n-1])
        u = L[n-1]
        return [u]+T        
    else:
        return L[:]

def main():
    L = [1,2,3,4,5]
    I = inverte(L)
    print(I)

main()
  

Solução 2:

def inverte(L):
    n = len(L)
    if n <= 1:
        return L[:] #return [ L[0] ] #return list(L)
    else:
        A = L[1:n]
        Ainv = inverte(A)
        Ainv.append(L[0])
        return Ainv
  

Problema 5: Torre de Hanoi

São dados um conjunto de n discos com diferentes tamanhos e três bases A, B e C.

O problema consiste em imprimir os passos necessários para transferir os discos da base A para a base B, usando a base C como auxiliar, nunca colocando discos maiores sobre menores.

Exemplo:

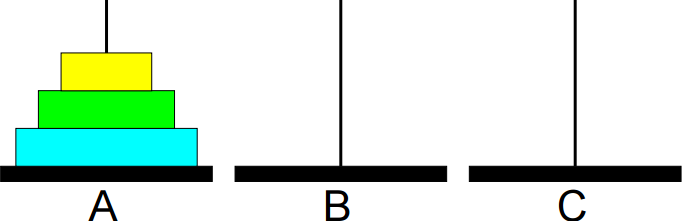
1º passo: Mover de A para B.

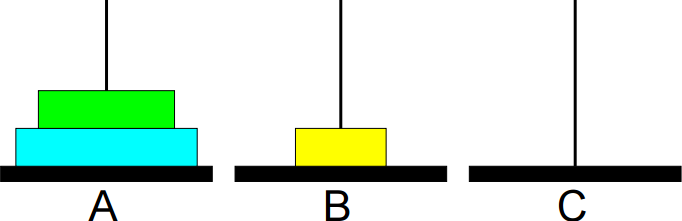
2º passo: Mover de A para C.

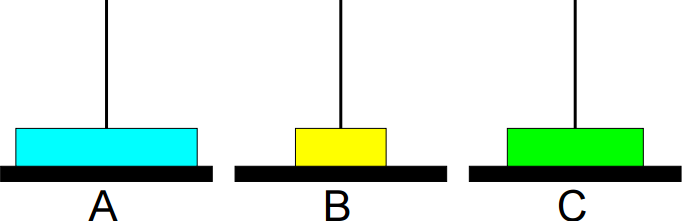
3º passo: Mover de B para C.

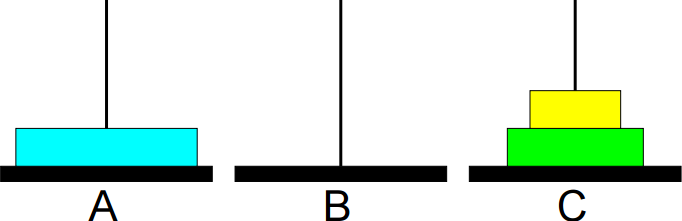
4º passo: Mover de A para B.

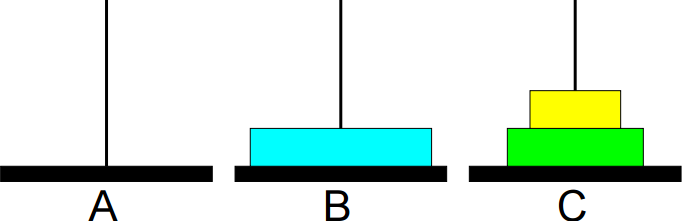
5º passo: Mover de C para A.

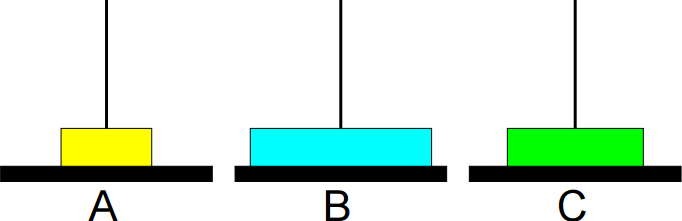
6º passo: Mover de C para B.

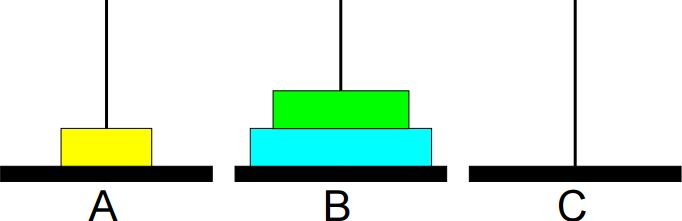
7º passo: Mover de A para B.

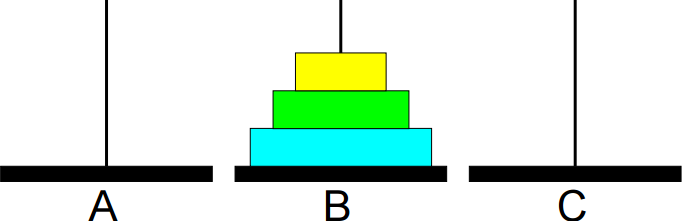
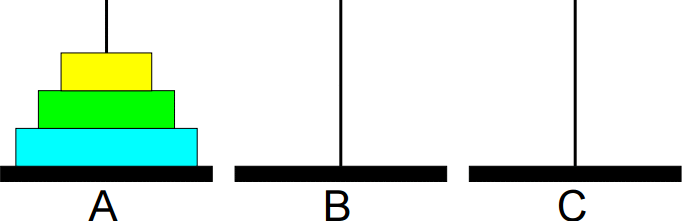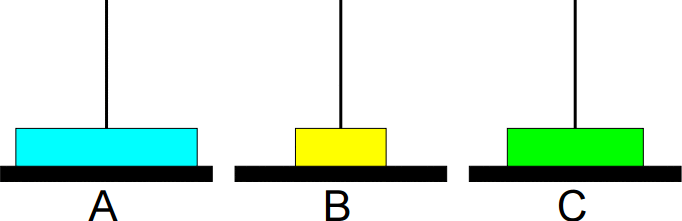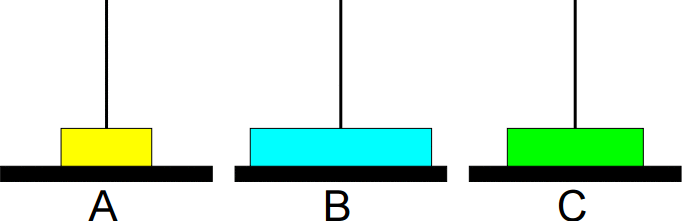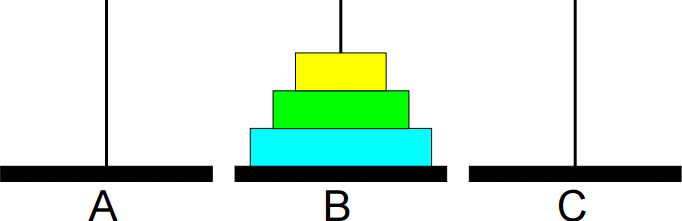
Animação da sequência completa de movimentos:

Solução:

def hanoi(n, orig, dest, aux):
  if n == 1:
    print("Mover de",orig,"para",dest)
  else:
    hanoi(n-1, orig, aux, dest)
    print("Mover de",orig,"para",dest)
    hanoi(n-1, aux, dest, orig)


def main():
  n = int(input("Digite a quantidade de discos: "))
  hanoi(n, "A", "B", "C")

main()