Aula 13: Matrizes

Tópicos

Aulas a distância - Google Meet:

Para verem os vídeos, vocês devem estar logados no e-mail da usp.

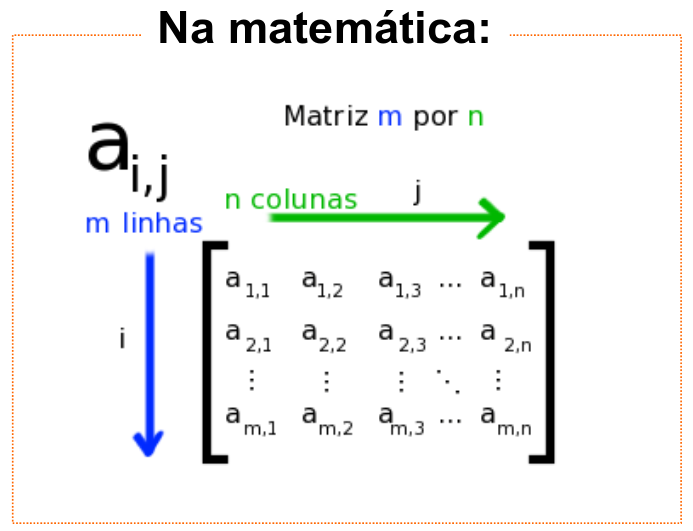
Em muitas aplicações, precisamos processar dados bidimensionais (gráfico cartesiano de coordenadas, imagens digitais, matrizes de sistemas de equações lineares em Álgebra Linear). Matriz é uma tabela organizada em linhas e colunas no formato m x n, onde m representa o número de linhas e n o número de colunas, tal como indicado na figura abaixo.

matriz

Criação explícita de matrizes em Python

Em Python, matrizes são definidas como listas de listas. Cada linha da matriz em Python é uma lista com n elementos. Por exemplo, o código abaixo cria uma matriz com três linhas e quatro colunas:
>>> A = [[4, 1, 8, 3],
         [2, 5, 7, 0],
         [6, 9, 0, 3]]

Índices

Na matemática, ai,j é o elemento que está na linha i e coluna j, com os índices iniciando no 1.

Em Python, os índices começam no zero. Logo, para acessar o elemento de valor 7 na matriz A definida acima, usamos i = 1 e j = 2. Para acessar um elemento da matriz na i-ésima linha e j-ésima coluna usamos a sintaxe: nome_matriz[i][j]
Exemplos:

>>> A[0][0]
4
>>> A[0][1]
1
>>> A[0][2]
8
>>> A[0][3]
3
>>> A[1][0]
2
>>> A[2][1]
9

A i-ésima linha da matriz pode ser obtida como uma lista usando a sintaxe: nome_matriz[i]
Exemplos:

>>> A[0]
[4, 1, 8, 3]
>>> A[1]
[2, 5, 7, 0]
>>> A[2]
[6, 9, 0, 3]

Dimensões de uma matriz

O número de linhas e colunas de uma matriz podem ser obtidos pela função len().

>>> len(A)      #número de linhas
3
>>> len(A[0])   #número de colunas
4

Criando matrizes de dimensões arbitrárias

O modo explícito de criação de matrizes, tal como apresentado anteriormente para a matriz A, é inadequado para a criação de matrizes maiores ou que possuem suas dimensões conhecidas apenas em tempo de execução.

Para criar uma matriz de dimensões arbitrárias, poderíamos pensar em usar o seguinte código:

>>> m = 3         #número de linhas
>>> n = 5         #número de colunas
>>> valor = 0         #valor inicial de preenchimento
>>> linha = [valor]*n
>>> matriz = [linha]*m
>>> print(matriz)
[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]

No entanto, ao modificar o valor do elemento matriz[0][0] na posição i = 0 e j = 0 da matriz obtemos o seguinte resultado:

>>> matriz[0][0] = 1
>>> print(matriz)
[[1, 0, 0, 0, 0], [1, 0, 0, 0, 0], [1, 0, 0, 0, 0]]

Observe que, estranhamente, os elementos matriz[1][0] e matriz[2][0] também tiveram seus valores alterados.
Isso ocorre porque o comando matriz = [linha]*m gerou uma matriz em que todas linhas são, na verdade, referências para a mesma lista na memória. Ou seja:

>>> id(matriz[0]) == id(matriz[1])
True
>>> id(matriz[0]) == id(matriz[2])
True

Para criar uma matriz de dimensões arbitrárias corretamente, podemos iniciar a matriz com a lista vazia [] e ir, em um laço, gradualmente adicionado suas linhas como clones da lista obtida via o comando linha = [valor]*n, tal como indicado no código abaixo: 

def cria_matriz(m, n, valor):
    matriz = []
    linha = [valor]*n
    for i in range(m):
        matriz.append(linha[:])
    return matriz
Podemos também criar cada uma das linhas a partir de uma lista vazia, usando uma estrutura de laços encaixados, tal como apresentado na solução alternativa abaixo: 
def cria_matriz(m, n, valor):
    matriz = []
    for i in range(m):
        linha = []
        for j in range(n):
            linha.append(valor)
        matriz.append(linha)
    return matriz

Manipulação de matrizes (soma):

Problema 1:

Escreva um programa que leia uma matriz de inteiros e que informa se ela é uma matriz simétrica. Uma matriz é simétrica se ela coincidir com a sua transposta. Observe que somente matrizes quadradas podem ser simétricas.

Solução: 

def main():
    A = leia_matriz()
    if simetrica(A):
        print("Matriz simétrica")
    else:
        print("Matriz não é simétrica")

def leia_matriz():
    nlinhas  = int(input("Digite o número de linhas: "))
    ncolunas = int(input("Digite o número de colunas: "))
    matriz = []
    for i in range(nlinhas):
        linha = []
        for j in range(ncolunas):
            num = int(input("Digite elem (%d,%d): "%(i,j)))
            linha.append(num)
        matriz.append(linha)
    return matriz

def simetrica(matriz):
    nlinhas = len(matriz)
    ncolunas = len(matriz[0])
    if nlinhas != ncolunas:
        return False
    for i in range(nlinhas):
        for j in range(i):
            if matriz[i][j] != matriz[j][i]:
                return False
    return True

main()

Problema 2:

Escreva um programa que leia inteiros positivos m e n e os elementos de uma matriz A de números inteiros de dimensão m x n e que conta o número de linhas e colunas que tem apenas zeros.

Exemplo: 

    Matriz: 4 x 5
         0  0  0  0  1
         0  0  0  0  0
         0  1  0  0  0
         0  0  0  0  0
Linhas nulas = 2
Colunas nulas = 3

Solução: 

def leia_matriz():
    m = int(input("Digite m: "))
    n = int(input("Digite n: "))
    matriz = []
    for i in range(m):
        linha = []
        for j in range(n):
            num = int(input("Digite elem (%d,%d): "%(i,j)))
            linha.append(num)
        matriz.append(linha)
    return matriz

def main():
    A = leia_matriz()
    m = len(A)
    n = len(A[0])
    lin_nulas,col_nulas = 0,0
    for i in range(m):
        zerada = True
        for j in range(n):
            if A[i][j] != 0:
                zerada = False
        if zerada:
            lin_nulas += 1

    for j in range(n):
        zerada = True
        for i in range(m):
            if A[i][j] != 0:
                zerada = False
        if zerada:
            col_nulas += 1

    print("Linhas nulas =",lin_nulas)
    print("Colunas nulas =",col_nulas)

main()

Problema 3:

Escreva um programa que calcula a multiplicação de duas matrizes A e B de números reais fornecidas.

Exemplo:

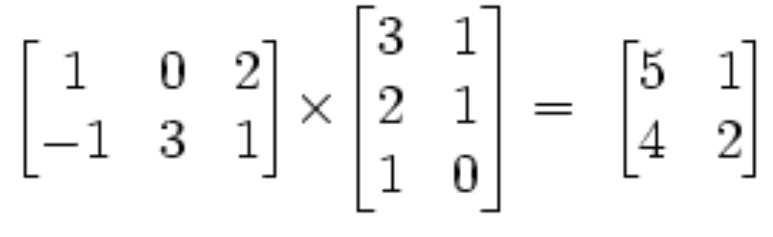
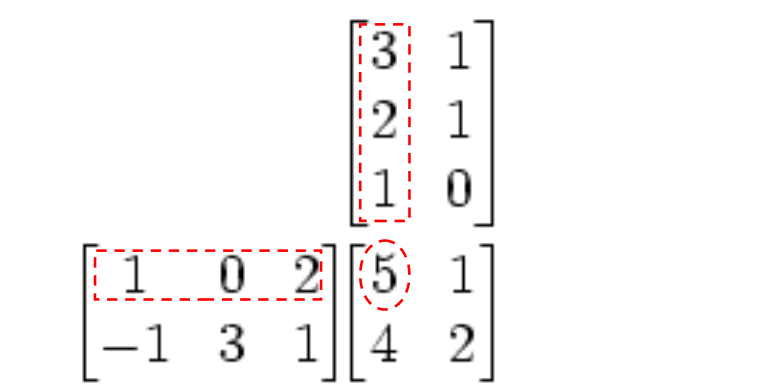
multiplicacao matrizes

Observe que o valor 5 na matriz de saída é calculado como 5 = 1*3 + 0*2 + 2*1.

multiplicacao matrizes 

def cria_matriz(nlinhas, ncolunas, valor):
    matriz = []
    for i in range(nlinhas):
        linha = []
        for j in range(ncolunas):
            linha.append(valor)
        matriz.append(linha)
    return matriz

def leia_matriz():
    nlinhas  = int(input("Digite o número de linhas: "))
    ncolunas = int(input("Digite o número de colunas: "))
    matriz = []
    for i in range(nlinhas):
        linha = []
        for j in range(ncolunas):
            num = float(input("Digite elem (%d,%d): "%(i,j)))
            linha.append(num)
        matriz.append(linha)
    return matriz

def imprima_matriz(matriz):
    nlinhas  = len(matriz)
    ncolunas = len(matriz[0])
    print("Matriz: %d x %d"%(nlinhas,ncolunas))
    for i in range(nlinhas):
        for j in range(ncolunas):
            print("%7.2f"%(matriz[i][j]), end="")
        print()

def main():
    A = leia_matriz()
    B = leia_matriz()
    if len(A[0]) != len(B):
        print("Matrizes incompatíveis")
        return
    m = len(A)
    n = len(A[0])
    p = len(B[0])
    C = cria_matriz(m, p, 0.0)
    for i in range(m):
        for j in range(p):
            C[i][j] = 0.0
            for k in range(n):
                C[i][j] += A[i][k]*B[k][j]
    imprima_matriz(C)

main()