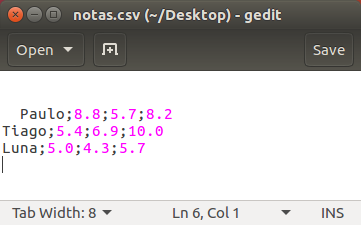
open() e método close().read(), readline() e readlines().for linha in arquivo:.write().Abaixo é mostrado um possível exemplo de arquivo de uma planilha no formato do CSV, contendo três alunos e suas respectivas notas das três provas:

Abaixo é apresentada uma solução:
def ordenacao(M):
n = len(M)
for n in range(len(M),1,-1):
imax = 0
for i in range(1,n):
if M[i][0] > M[imax][0]:
imax = i
tmp = M[n-1]
M[n-1] = M[imax]
M[imax] = tmp
def main():
#Leitura do arquivo de entrada
arquivo = open("notas.csv", 'r')
matriz = []
for linha in arquivo:
l = linha.strip()
if len(l) > 0:
palavras = l.split(";")
matriz.append(palavras)
arquivo.close()
ordenacao(matriz)
#Gravação do arquivo de saída
arquivo = open("notas2.csv", 'w')
n = len(matriz)
m = len(matriz[0])
for i in range(n):
for j in range(m-1):
arquivo.write(matriz[i][j])
arquivo.write(";")
arquivo.write(matriz[i][m-1])
arquivo.write("\n")
arquivo.close()
main()
Inicialmente, usamos a função open() para
abrir o arquivo de nome notas.csv para leitura, tal como indicado pelo
valor 'r' (do inglês read) do segundo parâmetro de open("notas.csv", 'r'). O arquivo notas.csv deve estar no mesmo diretório do programa sendo executado,
caso contrário devemos indicar explicitamente o caminho completo (path) do arquivo.
O comando for linha in arquivo: é então usado para
processar as linhas do arquivo, como se ele fosse uma lista de strings contendo as linhas do arquivo. Usamos o método strip() para eliminar o '\n' e demais caracteres considerados "brancos" (como o espaço e o tab) no início e final das linhas.
Adicionamos então na matriz as linhas não vazias do aquivo, como uma lista de palavras separadas por ; utilizando o método split(";").
Usamos então close para fechar o arquivo.
Para o exemplo fornecido, a seguinte matriz é obtida:
[['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0'], ['Luna', '5.0', '4.3', '5.7']]
A matriz é então ordenada pelo seu primeiro campo pela função ordenacao(). No exemplo, temos a seguinte matriz ordenada:
[['Luna', '5.0', '4.3', '5.7'], ['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0']]
A matriz ordenada é então gravada no disco. Para isso,
abrimos o arquivo de saída notas2.csv no modo gravação,
tal como indicado pelo valor 'w' (do inglês write) do segundo parâmetro
do comando open("notas2.csv", 'w').
O arquivo notas2.csv é gerado no mesmo diretório do programa sendo executado,
caso contrário devemos incluir todo o caminho (path) no seu nome.
Os elementos da matriz são gravados no disco usando
o método write(). Dado que o comando write()
não inclui automaticamente o caracter de quebra de linha,
devemos usar o "\n" explicitamente quando necessário.
Para o exemplo fornecido, temos o seguinte arquivo de saída:
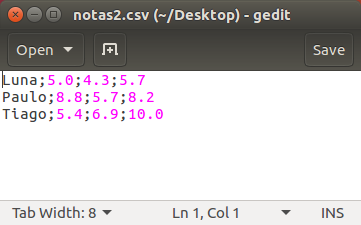
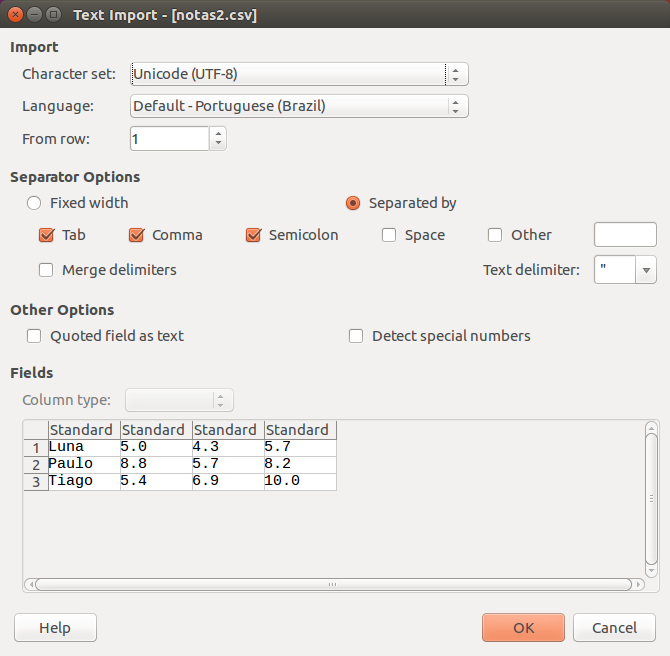
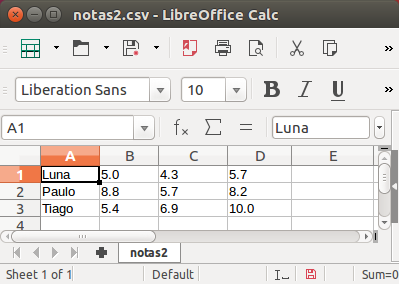
Arquivos no formato CSV são reconhecidos pelo OpenOffice/LibreOffice e programas similares. Abaixo mostramos o arquivo gerado sendo aberto no LibreOffice:
n > 0, faça uma
função molduras_concentricas(n, v1, v2) que gera
uma matriz quadrada nxn preenchida
com um padrão de molduras concêntricas, alternando entre
os dois valores fornecidos (v1 e v2) e iniciando com o valor v1 na
posição central da matriz,
tal como apresentado nos exemplos abaixo.
Para n=5, v1=0, v2=1:
[[0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 0, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0]]
Para n=7, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1]]
Para n=15, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
Solução:
#Cria matriz com m linhas e n colunas
def cria_matriz(m, n, valor):
M = []
for i in range(m):
linha = []
for j in range(n):
linha.append(valor)
M.append(linha)
return M
def molduras_concentricas(n, v1, v2):
M = cria_matriz(n, n, 0)
for i in range(n):
for j in range(n):
#dh = distancia horizontal ao centro
dh = n//2 - j
if dh < 0:
dh = -dh
#dv = distancia vertical ao centro
dv = n//2 - i
if dv < 0:
dv = -dv
if dh > dv:
if dh % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
else:
if dv % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
return M
def grava_PGM(M):
arquivo = open("fig01.pgm", 'w')
arquivo.write("P2\n")
m = len(M)
n = len(M[0])
arquivo.write("%d %d\n"%(n,m))
arquivo.write("255\n")
for i in range(m):
for j in range(n):
arquivo.write(" %3d"%(M[i][j]))
arquivo.write("\n")
arquivo.close()
def main():
n = int(input("Digite n: "))
M = molduras_concentricas(n, 0, 255)
grava_PGM(M)
main()
Invertendo o conteúdo das variáveis v1 e v2, obtemos uma imagem com o brilho invertido. Podemos gerar a gif animada abaixo, gravando essa segunda imagem em um arquivo fig02.pgm e usando o conversor de imagens do ImageMagick, executando no terminal o comando: convert -delay 10 *.pgm out.gif

A gif animada acima foi gerada usando n=101.
Que modificação você poderia fazer no código acima para obter molduras mais grossas como na figura abaixo?
