
Vamos usar a seguinte função auxiliar para criar uma matriz,
onde m é o número de linhas,
n é o número de colunas e
val é o valor inicial de preenchimento dos elementos da matriz.
def cria_matriz(m, n, val):
matriz = []
for i in range(m):
linha = []
for j in range(n):
linha.append(val)
matriz.append(linha)
return matriz
Para visualizar os resultados, vamos usar
a função abaixo que grava uma matriz
como uma imagem no formato PGM,
onde o valor zero indica o preto e o valor 255 indica o branco.
def grava_PGM(matriz, nomearquivo):
arquivo = open(nomearquivo, "w")
arquivo.write("P2\n")
m = len(matriz)
n = len(matriz[0])
arquivo.write("%d %d\n"%(n,m))
arquivo.write("255\n")
for i in range(m):
for j in range(n):
arquivo.write(" %3d"%(matriz[i][j]))
arquivo.write("\n")
arquivo.close()
(x1, y1) e (x2, y2) das extremidades
de um segmento de reta e uma matriz representando uma imagem em tons de cinza, faça uma função recursiva que desenha o segmento de reta na imagem com um valor de intensidade fornecido.
Solução:
Na solução abaixo,
o problema original é decomposto em dois subproblemas
de mesma natureza, dividindo o segmento ao meio
em dois segmentos menores.
A cada passo as coordenadas do ponto médio (xm, ym)
são calculadas e duas chamadas recursivas são realizadas.
A parada da recursão acontece quando
o problema se torna simples, envolvendo dois pontos vizinhos ou iguais.
Neste caso a solução trivial corresponde a pintar os dois pontos.
Note, no entanto, que somente podemos acessar posições da matriz
utilizando índices inteiros, caso contrário, teremos o seguinte erro:
list indices must be integers or slices, not float.
O arredondamento das coordenadas é obtido somando 0.5 antes de truncar os números (desprezar a parte fracionária) com o comando int().
def desenha_reta(matriz, x1,y1, x2,y2, val):
if abs(x2-x1) <= 1 and abs(y2-y1) <= 1:
matriz[int(y1+0.5)][int(x1+0.5)] = val
matriz[int(y2+0.5)][int(x2+0.5)] = val
else:
xm = (x1+x2)/2
ym = (y1+y2)/2
desenha_reta(matriz, x1,y1, xm,ym, val)
desenha_reta(matriz, xm,ym, x2,y2, val)
Exemplo de função principal que chama as
funções anteriores.
def main():
M = cria_matriz(240, 320, 0)
desenha_reta(M, 20,15, 300,210, 255)
grava_PGM(M, "reta.pgm")
main()
A figura abaixo apresenta o resultado da execução do programa acima.

OBS: Um algoritmo mais adequado para o desenho de linhas, em dispositivos matriciais, corresponde ao algoritmo de Bresenham.
O objetivo deste exercício é fazer um programa em Python, usando funções recursivas, para gerar imagens (no formato PGM) com os desenhos de um fractal conhecido como Tapete de Sierpinski.
A construção do Tapete de Sierpinski parte de um quadrado, que é subdividido em nove partes. A parte central é removida, de modo que sobram então oito pequenos quadrados. Para cada um deles, é aplicado o mesmo processo de divisão em nove partes, retirando a parte central, e assim sucessivamente. Este processo pode ser repetido infinitamente, mas no contexto de imagens a repetição é feita até atingir um número máximo de iterações.
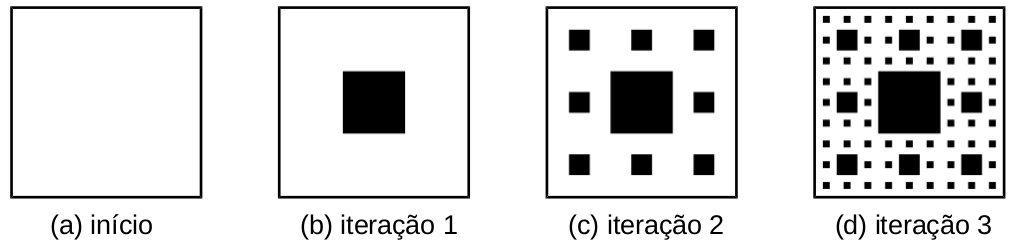
Solução:
A função tapete_sierpinski(n, niveis)
gera uma imagem quadrada nxn do tapete de Sierpinski,
onde niveis é o número máximo de iterações e o quadrado inicial do tapete corresponde a toda a imagem.
A função recursiva tapete_sierpinski_aux(matriz, x1,y1, x2,y2, niveis) realiza a divisão do quadrado, compreendido entre as coordenadas
(x1,y1) e (x2,y2), em nove partes e pinta a parte central de preto, conforme a ilustração abaixo.
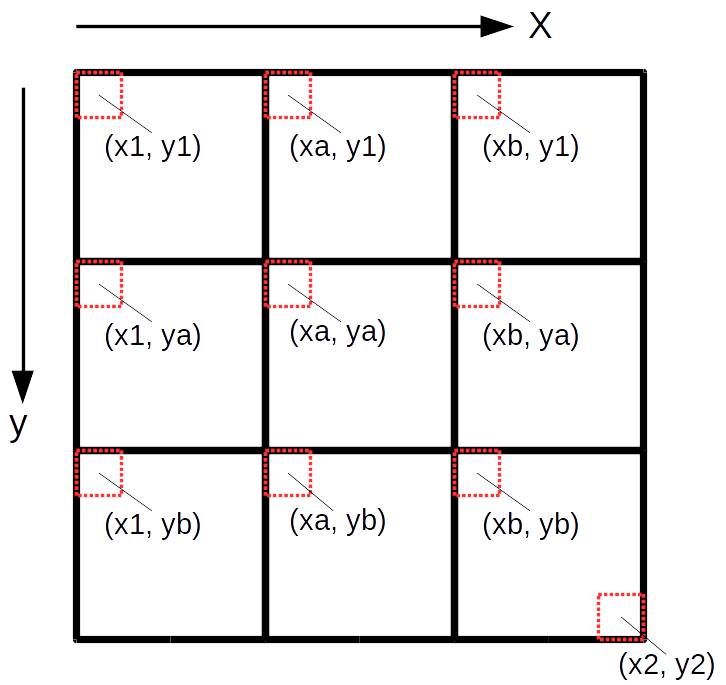
def tapete_sierpinski_aux(matriz, x1,y1, x2,y2, niveis):
if niveis > 0:
tam = x2-x1+1
xa = x1 + tam//3
xb = xa + tam//3
ya = y1 + tam//3
yb = ya + tam//3
tapete_sierpinski_aux(matriz, x1,y1, xa-1,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, x1,ya, xa-1,yb-1, niveis-1)
tapete_sierpinski_aux(matriz, x1,yb, xa-1,y2, niveis-1)
tapete_sierpinski_aux(matriz, xa,y1, xb-1,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, xa,yb, xb-1,y2, niveis-1)
tapete_sierpinski_aux(matriz, xb,y1, x2,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, xb,ya, x2,yb-1, niveis-1)
tapete_sierpinski_aux(matriz, xb,yb, x2,y2, niveis-1)
for i in range(ya,yb):
for j in range(xa,xb):
matriz[i][j] = 0
def tapete_sierpinski(n, niveis):
M = cria_matriz(n, n, 255)
tapete_sierpinski_aux(M, 0,0, n-1,n-1, niveis)
return M
Exemplo de função principal que chama as
funções anteriores, considerando uma imagem quadrada nxn,
onde n é uma potência de três (ex: 3^6 = 729) e
o nome do arquivo de saída é tapete.pgm.
def main():
n = 3**6
T = tapete_sierpinski(n, 5)
grava_PGM(T, "tapete.pgm")
main()
A figura abaixo apresenta o resultado da execução do programa acima.
