Operadores Aritméticos de Atribuição +=,-=,*=,/=,%=

Cada um destes operadores é usado com um nome de variável à sua esquerda e uma expressão à sua direita.

Operador	Exemplo	É equivalente a:
*=	x *= 5	x = x * 5
/=	x /= 5	x = x / 5
%=	x %= 5	x = x % 5
+=	x += 5	x = x + 5
-=	x -= 5	x = x - 5

Operadores / e % com inteiros (Divisão inteira e Resto)

Operador	Nome	Explicação	Exemplos
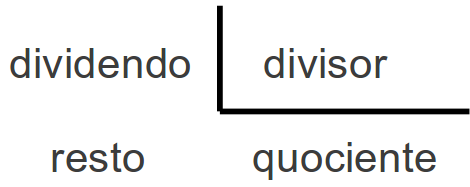
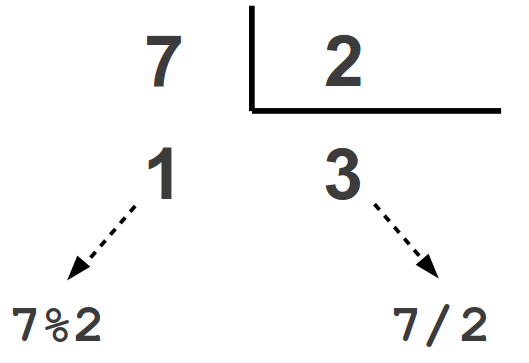
/	Divisão Inteira	Retorna a parte inteira do quociente	4 / 3 retorna 1
%	Módulo	Retorna o resto da divisão	8% 3 retorna 2

Problema 1:

Dados um número inteiro n, n > 0, e um dígito d (0 ≤ d ≤ 9), determinar quantas vezes d ocorre em n. Por exemplo, 3 ocorre 2 vezes em 63453.

#include <stdio.h>

int main(){
  int n,nn,d,r,cont=0;

  printf("Digite o valor de n: ");
  scanf("%d",&n);
  nn = n;
  printf("Digite um dígito [0,9]: ");
  scanf("%d",&d);

  while(n != 0){
    r = n % 10;
    if(r == d)
      cont = cont + 1;
    n = n / 10;
  }
  n = nn;
  printf("%d ocorre %d vezes em %d.\n",d,cont,n);
  return 0;
}

Problema 2:

Dado um número inteiro n>0, verificar se este número contém dois dígitos adjacentes iguais.

#include <stdio.h>

int main(){
  int n,r,ant,adjiguais = 0;

  printf("Digite o valor de n: ");
  scanf("%d",&n);
  ant = n % 10;
  n = n / 10;  
  while(n > 0){
    r = n % 10;
    if(ant == r)
      adjiguais = 1;
    ant = r;
    n = n / 10;
  }
  if(adjiguais)
    printf("Contém adjacentes iguais.\n");
  else
    printf("Não contém adjacentes iguais.\n");

  return 0;
}

Uma segunda solução usando uma condição extra de parada do laço.
Quando adjiguais recebe 1 (Verdadeiro), seu valor não é mais alterado, logo não há necessidade de continuar o laço nesse caso:

#include <stdio.h>

int main(){
  int n,r,ant,adjiguais = 0;

  printf("Digite o valor de n: ");
  scanf("%d",&n);
  ant = n % 10;
  n = n / 10;  
  while(n > 0 && !adjiguais){
    r = n % 10;
    if(ant == r)
      adjiguais = 1;
    ant = r;
    n = n / 10;
  }
  if(adjiguais)
    printf("Contém adjacentes iguais.\n");
  else
    printf("Não contém adjacentes iguais.\n");

  return 0;
}

Outra solução alternativa, inicializando a variável ant com um dígito inválido, ao invés de ler o primeiro dígito de n fora do laço. Com essa alteração, a condição do laço ant == r nunca será verdadeira na primeira iteração do laço.

#include <stdio.h>

int main(){
  int n,r,ant,adjiguais = 0;

  printf("Digite o valor de n: ");
  scanf("%d",&n);
  ant = 10; /*dígito inválido > 9*/
  while(n > 0 && !adjiguais){
    r = n % 10;
    if(ant == r)
      adjiguais = 1;
    ant = r;
    n = n / 10;
  }
  if(adjiguais)
    printf("Contém adjacentes iguais.\n");
  else
    printf("Não contém adjacentes iguais.\n");

  return 0;
}

Problema 3:

Qualquer número natural de quatro algarismos pode ser dividido em duas dezenas formadas pelos seus dois primeiros e dois últimos dígitos.
Exemplos:

1297: 12 e 97.
5314: 53 e 14.

Escreva um programa que imprime todos os milhares (4 algarismos) cuja raiz quadrada seja a soma das dezenas formadas pela divisão acima.

Exemplo: raiz de 9801 = 99 = 98 + 01.
Portanto 9801 é um dos números a ser impresso.

#include <stdio.h>

int main(){
  int i,d1,d2;

  for(i = 1000; i <= 9999; i += 1){
    d1 = i%100;
    d2 = i/100;
    if( (d1+d2)*(d1+d2) == i )
      printf("%d\n",i);
  }
  return 0;
}

Problema 4:

Dados números inteiros n, i e j, todos maiores do que zero, imprimir em ordem crescente os n primeiros naturais que são múltiplos de i ou de j e ou de ambos. Por exemplo, para n=6, i=2 e j=3 a saída deverá ser:

    0    2    3   4    6    8

Primeira solução: Testa os números 0, 1, 2, ... verificando e imprimindo quais são múltiplos de i ou j, até que n múltiplos sejam impressos.

#include <stdio.h>

int main(){
  int n,i,j,cont,cm;
  printf("Cálculo dos n primeiros múltiplos de i ou de j\n");
  /*Dados de entrada:*/
  printf("Digite n: ");
  scanf("%d",&n);
  printf("Digite i: ");
  scanf("%d",&i);
  printf("Digite j: ");
  scanf("%d",&j);
  cm = 0;   /*candidato a múltiplo.*/
  cont = 0; /*conta quantos múltiplos foram impressos.*/
  while(cont < n){
    if(cm%i == 0 || cm%j == 0){
      printf("%d ",cm);
      cont += 1;
    }
    cm += 1;
  }
  printf("\n");
  return 0;
}

Segunda solução: Mais elaborada. Faz menos iterações que a anterior. A cada iteração imprime um múltiplo de i ou j.

#include <stdio.h>

int main(){
  int n,i,j,multi,multj,cont;
  printf("Cálculo dos n primeiros múltiplos de i ou de j\n");
  /*Dados de entrada:*/
  printf("Digite n: ");
  scanf("%d",&n);
  printf("Digite i: ");
  scanf("%d",&i);
  printf("Digite j: ");
  scanf("%d",&j);
  multi = 0; /*múltiplos de i*/
  multj = 0; /*múltiplos de j*/
  cont = 0;  /*conta quantos múltiplos foram impressos.*/
  while(cont < n){
    if(multi < multj){
      printf("%d ",multi);
      multi += i;
    }
    else if(multj < multi){
      printf("%d ",multj);
      multj += j;      
    }
    else{  /*multi == multj*/
      printf("%d ",multj);
      multi += i;
      multj += j;
    }
    cont += 1;
  }
  return 0;
}

Problema 5:

Dado um número inteiro n, n>0, verificar se n é primo.

Um número natural é um número primo quando ele tem exatamente dois divisores naturais distintos: o número um e ele mesmo. Por definição, 0 e 1 não são números primos.

Primeira solução:
Um número primo n não pode ser divisível por nenhum outro número no intervalo [2,n-1]. Logo, testamos todos candidatos a divisores possíveis no intervalo [2,n-1], e usamos um indicador de passagem (variável primo) para sinalizar a ocorrência desse evento (divisão). Ao final do programa vale que primo == 0 se e somente se o número dado não é primo.

#include <stdio.h>

int main(){
  int n,d,primo;
  printf("Teste de primalidade\n");
  printf("Digite um inteiro: ");
  scanf("%d",&n);
  /*o número é primo até que se prove o contrário*/
  primo = 1; /*indicador de passagem*/
  d = 2;  /*os candidatos a divisores positivos de n*/
  while(d < n){
    if(n%d == 0)
      primo = 0; /*não é primo!*/
    d += 1;
  }
  if(n <= 1)  /*nenhum número natural <= 1 é primo.*/
    primo = 0;

  if(primo)
    printf("O número é primo\n");
  else
    printf("O número não é primo\n");

  return 0;
}

Segunda solução: Reduz o espaço de busca, testando apenas os candidatos a divisores positivos de n no intervalo 2,3,4,...,n/2.

#include <stdio.h>

int main(){
  int n,d,primo;
  printf("Teste de primalidade\n");
  printf("Digite um inteiro: ");
  scanf("%d",&n);
  /*o número é primo até que se prove o contrário.*/
  primo = 1; /*indicador de passagem*/

  if(n <= 1)  /*nenhum número natural <= 1 é primo.*/
    primo = 0;
  d = 2;  /*os candidatos a divisores positivos de n.*/
  while(d <= n/2 && primo){
    if(n%d == 0)
      primo = 0;  /*não é primo!*/
    d += 1;
  }
  if(primo)
    printf("O número é primo\n");
  else
    printf("O número não é primo\n");

  return 0;
}

Terceira solução: Reduz o espaço de busca ainda mais. Testa se o número é par fora do laço principal. Dentro do while só testa candidatos a divisores ímpares.

#include <stdio.h>

int main(){
  int n,d,primo;
  printf("Teste de primalidade\n");
  printf("Digite um inteiro: ");
  scanf("%d",&n);
  if(n <= 1)  /*nenhum número natural <= 1 é primo.*/
    primo = 0;
  else if(n%2==0 && n > 2) 
    primo = 0;   /*nenhum número par > 2 é primo.*/
  else         /*o número é primo até que se prove o contrário*/
    primo = 1; /*vale que n é um ímpar maior que 1 ou é 2.*/

  d = 3; /* os candidatos a divisores positivos de n são 3,5,7,...,n/2 */
  while(d <= n/2 && primo){
    if(n%d == 0)
      primo = 0;  /*não é primo!*/
    d += 2;
  }
  if(primo)
    printf("O número é primo\n");
  else
    printf("O número não é primo\n");

  return 0;
}

Outras possíveis otimizações podem ser encontradas aqui.

Problema 6:

Dados dois inteiros calcular o máximo divisor comum (MDC) entre eles.

O MDC de dois números inteiros é o maior número inteiro que divide ambos sem deixar resto.

Exemplos:

MDC(24,15) = 3.
MDC(252,105) = 21.
MDC(80,120) = 40.

#include <stdio.h>

int main(){
  int a,b,m,i,mdc=1;
  printf("MDC entre A e B:\n");
  printf("Entre com A: ");
  scanf("%d",&a);
  printf("Entre com B: ");
  scanf("%d",&b);
  if(a == 0 && b == 0){
    printf("MDC(0, 0) não existe pois todo inteiro não-nulo é divisor de zero.\n");
    return 0;
  }
  else if(a == 0)
    mdc = b;
  else if(b == 0)
    mdc = a;
  else{
    if(a < b)
      m = a;
    else
      m = b;
  
    for(i=2; i <= m; i++){
      if(a%i == 0 && b%i == 0)
        mdc = i;
    }
  }
  printf("MDC = %d\n",mdc);
  return 0;
}

Segunda solução: Nessa segunda solução, realizamos o laço a partir do maior valor candidato a MDC em direção aos menores, o que permite encerrar o laço assim que o primeiro divisor comum for encontrado. Será assumido que a > 0 e b > 0 a fim de simplificar o código.

#include <stdio.h>

int main(){
  int a,b,m;
  printf("MDC entre A e B:\n");
  printf("Entre com A: ");
  scanf("%d",&a);
  printf("Entre com B: ");
  scanf("%d",&b);

  if(a < b)
    m = a;
  else
    m = b;

  for(; m > 0 ; m--){
    if(a%m == 0 && b%m == 0)
      break;
  }
  printf("MDC = %d\n",m);
  return 0;
}

Terceira solução: Dados dois inteiros positivos calcular o máximo divisor comum (MDC) entre eles usando o algoritmo de Euclides.

Algoritmo de Euclides: Para dois números A e B:

Se A ≥ B: MDC(A,B) = MDC(A-B, B) = MDC(A%B, B) = MDC(B, A%B)
Se A < B: MDC(A,B) = MDC(B,A)

A repetição deste processo irá gerar sucessivamente números menores, até convergir em zero. Nesse momento, o MDC é o outro número inteiro, maior que zero.

#include <stdio.h>

int main(){
  int a,b,r,t;
  printf("MDC entre A e B:\n");
  printf("Entre com A: ");
  scanf("%d",&a);
  printf("Entre com B: ");
  scanf("%d",&b);

  if(a < b){
    t = a;
    a = b;
    b = t;
  }
  while(b > 0){
    r = a%b;
    a = b;
    b = r;
  }
  printf("MDC = %d\n",a);
  return 0;
}

Na verdade o primeiro "if" não é necessário e pode ser omitido, pois a primeira iteração do laço irá naturalmente inverter o conteúdo das variáveis a e b quando a < b.

#include <stdio.h>

int main(){
  int a,b,r;
  printf("MDC entre A e B:\n");
  printf("Entre com A: ");
  scanf("%d",&a);
  printf("Entre com B: ");
  scanf("%d",&b);

  while(b > 0){
    r = a%b;
    a = b;
    b = r;
  }
  printf("MDC = %d\n",a);
  return 0;
}