Custo de caminhos entre cidades:

A seguir, mostraremos um exemplo de aplicação de filas para calcular distâncias entre cidades. Considere um conjunto de N cidades, sendo que algumas estão interligadas por vias diretas de mão única (Fig.1). Inicialmente vamos supor que todas estradas existentes possuem o mesmo custo de transporte.

Fig.1Fig.2Fig.3

Primeiramente vamos considerar uma camada de abstração utilizando o conceito matemático de grafos.
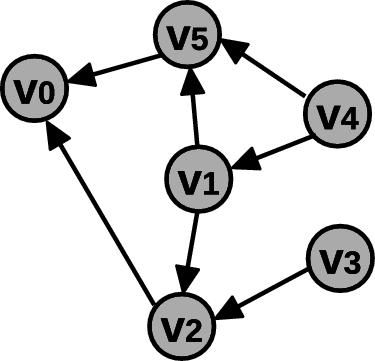
Um grafo orientado, ou grafo dirigido, G(V,A) é definido pelo par de conjuntos V e A, onde:

Por exemplo, no nosso problema de N cidades (numeradas de 0 a N-1) temos o grafo da Fig.2, onde: Uma das formas de representar um grafo, em linguagem C, é através da sua matriz de adjacência (Fig.3). Uma matriz de adjacência A é uma matriz quadrada NxN, onde os valores de A[i][j] são iguais a 1 se os vértices vi e vj são adjacentes, isto é, (vi,vj) ∈ A, e 0 caso contrário.

Um caminho no grafo é uma sequência de vértices adjacentes (de cada um dos vértices existe uma aresta para o vértice seguinte).
O comprimento do caminho é o número de arestas que o caminho usa. No nosso problema, o caminho é uma sequência de cidades, interligadas por vias diretas, a partir de uma cidade de origem até uma cidade de destino.

A importância do uso da abstração por grafos reside no fato de que muitos problemas provenientes de diversas áreas podem ser tratados com o uso de algoritmos comuns em grafos, permitindo o reaproveitamento do código.

Para resolver o problema dos caminhos de menor comprimento a partir de uma cidade de origem, considere o arquivo de código abaixo contendo a implementação de uma fila usando listas ligadas circulares.

Arquivo: fila_lig.c
typedef enum boolean {false,true} bool;

typedef struct _RegFila{
  TipoDado         dado;
  struct _RegFila *prox;
} RegFila;

typedef RegFila* Fila;

RegFila *AlocaRegFila(){
  RegFila* q;
  q = (RegFila*)calloc(1, sizeof(RegFila));
  if(q==NULL) exit(-1);  
  return q;
}

Fila     CriaFila(){
  Fila p;
  p = AlocaRegFila();
  p->prox = p;
  return p;
}

void     LiberaFila(Fila p){
  RegFila *q,*t;
  q = p->prox;
  while(q!=p){
    t = q;
    q = q->prox;
    free(t);
  }
  free(p);
}

bool     FilaVazia(Fila p){
  return (p==p->prox);
}

void     InsereFila(Fila *p, TipoDado x){
  RegFila *q;
  q = AlocaRegFila();
  q->dado = x;
  q->prox = (*p)->prox;
  (*p)->prox = q;
  *p = q;
}

TipoDado RemoveFila(Fila *p){
  RegFila *q,*t;
  TipoDado x;
  q = (*p)->prox;
  if(q==*p) exit(-1); /* Fila Vazia */
  t = q->prox;
  x = t->dado;
  q->prox = t->prox;
  if(t==*p) *p = q;
  free(t);
  return x;
}

Comprimento dos menores caminhos a partir de uma cidade de origem:

Função que calcula os comprimentos dos menores caminhos a partir de uma cidade de origem para as outras cidades. 
/* Numero de cidades consideradas */
#define N 6

void Comprimentos(int A[N][N], 
                  int orig, int C[N]) {
  Fila f;
  int i,j;
  f = CriaFila();
  for (i = 0; i < N; i++)
    C[i] = INT_MAX;

  C[orig] = 0;
  InsereFila(&f, orig);

  while ( !FilaVazia(f) ) {
    i = RemoveFila(&f);

    for (j = 0; j < N; j++) {
      if (A[i][j] == 1 && C[j] == INT_MAX) {
        C[j] = C[i] + 1;
        InsereFila(&f, j);
      }
    }
  }
  LiberaFila(f);
}

Caminho de comprimento mínimo entre cidade de origem e destino:

Função que calcula um caminho de comprimento mínimo entre uma cidade de origem e uma cidade de destino. 
void Caminho(int A[N][N], 
             int orig, 
             int dest,
             int C[N],
             int P[N]) {
  Fila f;
  int i,j;
  f = CriaFila();
  for (i = 0; i < N; i++) {
    C[i] = INT_MAX;
    P[i] = -1;
  }

  D[orig] = 0;
  InsereFila(&f, orig);

  while ( !FilaVazia(f) ) {
    i = RemoveFila(&f);

    if (i == dest) break;

    for (j = 0; j < N; j++) {
      if (A[i][j] == 1 && C[j] == INT_MAX){
        C[j] = C[i] + 1;
        P[j] = i;
        InsereFila(&f, j);
      }
    }
  }
  LiberaFila(f);
}

Exemplo de função principal main:

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

/* Numero de cidades consideradas */
#define N 6

/* Para utilizar as funcoes de manipulacao de fila 
   presentes no arquivo fila_lig.c */
typedef int TipoDado;
#include "fila_lig.c"


/* Inserir nesse ponto o código das demais funções anteriores */


int main() {
/*
  A[i][j] indica se existe caminho direto da 
  cidade i para a cidade j.
*/
  int A[N][N] = {{0,0,0,0,0,0},
                 {0,0,1,0,0,1},
                 {1,0,0,0,0,0},
                 {0,0,1,0,0,0},
                 {0,1,0,0,0,1},
                 {1,0,0,0,0,0} };
/* C[i] vai armazenar o comprimento minimo de caminho
   de uma cidade de origem ate a cidade i */
  int C[N]; 
/* P[i] sera a cidade predecessora de i no  
   caminho otimo calculado, ou P[i] == -1 se i for
   a cidade de origem */
  int P[N];
/* Vetor auxiliar temporario */
  int T[N]; 
  int i,j;
  int orig, dest;

/* Calcula os menores valores de comprimento para
   todas cidades a partir de uma cidade de origem 
   (cidade 4 no exemplo abaixo) */
  orig = 4;
  Comprimentos(A, orig, C);

/* Imprime os comprimentos calculados: */
  for (i = 0; i < N; i++) {
    if (C[i] == INT_MAX)
      printf(" MAX");
    else
      printf(" %d", C[i]);
  }
  printf("\n");

/* Calcula um caminho de comprimento minimo entre uma 
   cidade de origem e uma cidade de destino fornecidas 
   (4 e 0 no exemplo) */
  dest = 0;
  Caminho(A, orig, dest, C, P);

/* Copia as cidades percorridas no sentido inverso
   (que é dado pelo mapa de predecessores) no vetor T */
  j = 0;
  i = dest;
  while ( i != -1 ) {
    T[j] = i;
    j++;
    i = P[i];
  }

/* Imprime cidades percorridas no sentido correto 
   de orig para dest */
  j--;
  for ( ; j >= 0; j--) {
    printf(" %d", T[j]);
  }
  printf("\n");

  return 0;
}

Custo de caminhos entre cidades em grafos com pesos nas arestas:

Imagine agora que o conjunto de N cidades numeradas de 0 a N-1 são interligadas por estradas que possuem um custo de transporte (distância, pedágios, etc). Nesse caso, A[i][j] pode conter, ao invés de 1 quando houver uma aresta entre vi e vj, o peso dessa mesma aresta (isto é, o custo de transporte da cidade vi para a cidade vj). Valores de A[i][j] nulos são usados para indicar a ausência de uma via direta da cidade vi para a cidade vj. Um grafo com pesos nas arestas é chamado de grafo valorado ou grafo ponderado.

O custo de um caminho num grafo ponderado é a soma dos custos das arestas atravessadas. Para encontrar de modo eficiente os caminhos de custo mínimo podemos usar o Algoritmo de Dijkstra, e quando conhecemos de antemão qual é a cidade de destino, podemos usar o Algoritmo A* (Lê-se: A-estrela). Esses algoritmos são mais sofisticados e utilizam filas de prioridade. Aqui iremos apenas discutir uma possível solução menos eficiente para o problema usando filas simples (no caso quando os pesos são valores inteiros) que reutiliza os códigos vistos acima.

A idéia é criar um grafo não-ponderado com vértices adicionais, de modo que os comprimentos dos caminhos nesse novo grafo correspondam aos custos dos caminhos para pares de vértices correspondentes no primeiro grafo. Por exemplo, um arco de peso 3 de vi para vj deverá ser trocado por três arcos não-ponderados, sendo necessária a criação de duas cidades fictícias (vértices adicionais) entre vi e vj. Logo, podemos calcular os comprimentos dos caminhos no novo grafo, consequentemente resolvendo o problema dos custos do primeiro grafo ponderado.