Laços aninhados (repetições encaixadas)

Exemplo 1:

Mostrar uma pirâmide semelhante a abaixo, sendo que o maior valor da pirâmide é definido pelo usuário. Ex: n=9 
9 8 7 6 5 4 3 2 1 
8 7 6 5 4 3 2 1 
7 6 5 4 3 2 1 
6 5 4 3 2 1 
5 4 3 2 1 
4 3 2 1 
3 2 1 
2 1 
1 

n = int(input("Digite n: "))

j = n
while j > 0:
    i = j
    while i > 0:
        print(i,end=" ")
        i -= 1
    print()
    j -= 1

Exemplo 2:

Dado um número inteiro n (n>1), e um número inteiro m (m>1), faça um programa que calcula o resultado da soma:
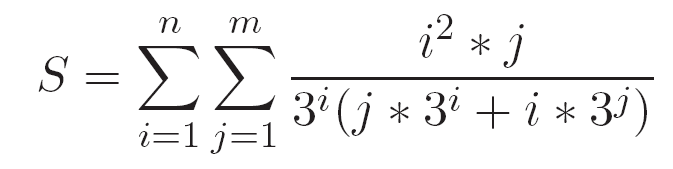
somatorio 

soma = 0
i = 1
while i <= n:
    j = 1
    while j <= m:
        #numerador:
        num = i*i*j 
        #denominador:
        den = (3**i)*(j*(3**i) + i*(3**j))
        soma += num/den
        j += 1
    i += 1

print("Soma:",soma)
Uma solução alternativa pode ser obtida através da manipulação dos somatórios:

somatorio 

soma = 0
i = 1
while i <= n:
    somaj = 0
    pi = 3**i
    j = 1
    while j <= m:
        somaj += j/(j*pi + i*(3**j))
        j += 1
    soma += (i*i/pi)*somaj
    i += 1

print("Soma:",soma)

Problema 1:

Dado um número inteiro n, n>1, imprimir sua decomposição em fatores primos, indicando também a mutiplicidade de cada fator. Por exemplo, para n=600, a saída deverá ser: 
n = int(input("Digite n: "))
print("Decomposição de",n,"em fatores primos:")

fator = 2
while n > 1:
    mult = 0
    while n%fator == 0:
        n = n//fator
        mult += 1
    if mult > 0:
        print("fator",fator,"multiplicidade",mult)
    fator += 1

Problema 2:

Dados um número inteiro n>0 e uma sequência com n números inteiros maiores do que zero, determinar o máximo divisor comum entre eles. Por exemplo, para a entrada 
3 42 30 105
o seu programa deve escrever o número 3.

DICA: O MDC é uma operação associativa: 

MDC(A,B,C,D) = MDC(MDC(A,B),C,D) = MDC(MDC(MDC(A,B),C),D)

n = int(input("Digite n: "))
mdc = int(input("Digite um num: "))
i = 1
while i < n:
    num = int(input("Digite um num: "))
    a = mdc
    b = num
    #MDC entre A e B:
    if a < b:
        a,b = b,a
    while b > 0:
        r = a%b
        a = b
        b = r
    mdc = a
    i += 1

print("MDC =",mdc)