
Uma função é dita recursiva quando dentro dela é feita uma ou mais chamadas a ela mesma.
A ideia é dividir um problema original um subproblemas menores de mesma natureza (divisão) e depois combinar as soluções obtidas para gerar a solução do problema original de tamanho maior (conquista). Os subproblemas são resolvidos recursivamente do mesmo modo em função de instâncias menores, até se tornarem problemas triviais que são resolvidos de forma direta, interrompendo a recursão.
Solução 1:
Solução não recursiva.
def fatorial(n):
fat = 1
while n > 1:
fat *= n
n -= 1
return fat
Solução 2:
Solução recursiva: n! = n.(n-1)!

def fatorial(n):
if n == 0: #Caso trivial
return 1 #Solução direta
else:
return n*fatorial(n-1) #Chamada recursiva

Exemplo da sequência:
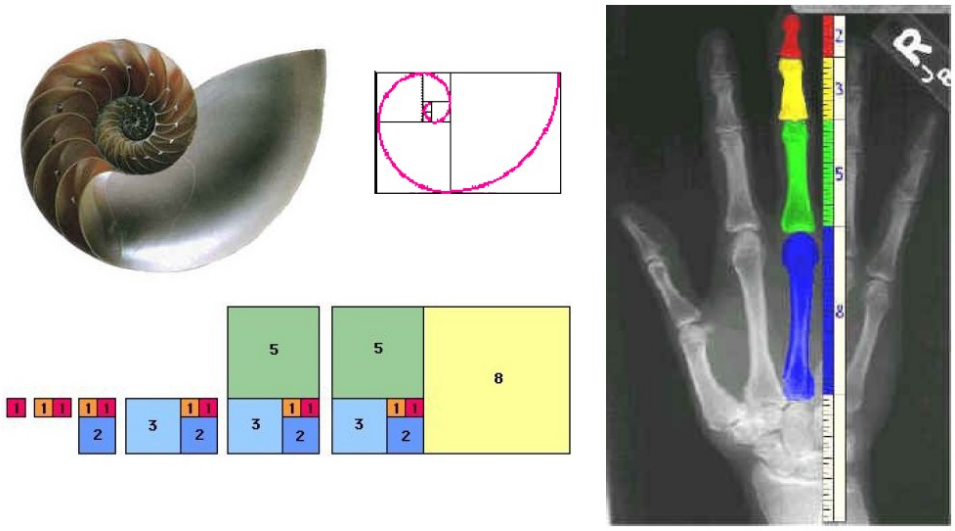
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...A ocorrência da sucessão de Fibonacci na natureza é tão frequente que é difícil acreditar que seja acidental (ex: flores, conchas, mão humana).
Solução 1:
Versão recursiva:
def fibo(n):
if n <= 1:
return n
else:
return fibo(n-1) + fibo(n-2)
Solução 2:
Versão não recursiva:
def fibo(n):
f0 = 0
f1 = 1
for k in range(1,n+1):
f2 = f0 + f1
f0 = f1
f1 = f2
return f0
Análise de eficiência das funções
Fibonacci calculando o número de operações
de soma S(n) realizadas:

Neste caso não faz sentido utilizar a versão recursiva.
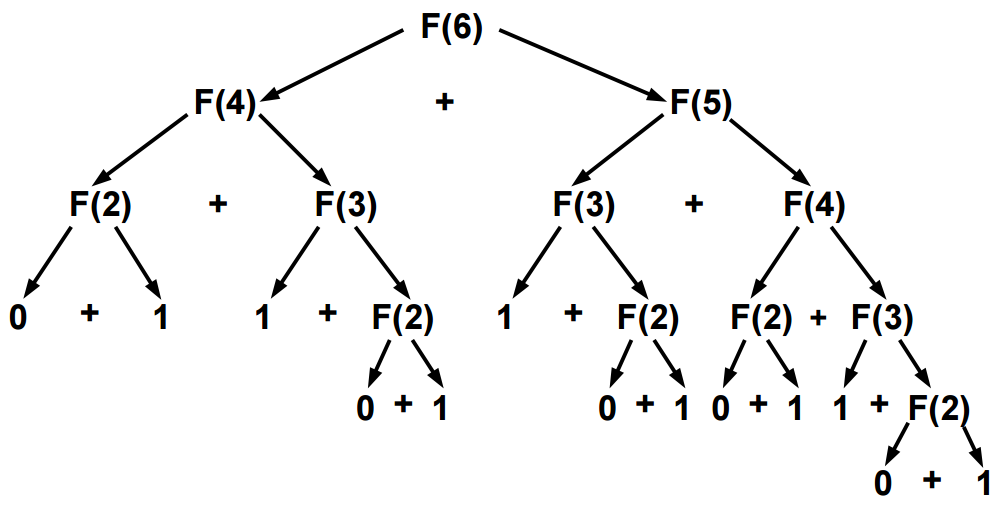
Árvore de Recorrência:
A solução recursiva é ineficiente, pois recalcula várias vezes a solução para valores intermediários:
Por exemplo, para F(6)=fibo(6) = 8, temos 2xF(4), 3xF(3), 5xF(2).
x elevado a n positivo.
Solução 1:
Solução não recursiva.
def potencia(x, n):
pot = 1.0
while n > 0:
pot *= x
n -= 1
return pot
Solução 2:
Solução recursiva: x^n = x . x^(n-1)
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0 #Solução direta
else:
return x*potencia(x, n-1) #Chamada recursiva
Solução 3:
Solução recursiva: x^n = x^(n/2). x^(n/2) = (x^(n/2))^2
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0
elif n%2 == 0: #Se n é par...
pot = potencia(x, n//2)
return pot*pot
else: #Se n é ímpar...
pot = potencia(x, n//2)
return pot*pot*x
Solução:
#Encontra o maior valor de uma lista com n elementos.
def maiorinteiro_aux(L, n):
if n==1: #Caso trivial
return L[0]
else:
m = maiorinteiro_aux(L, n-1)
if m > L[n-1]:
return m
else:
return L[n-1]
def maiorinteiro(L):
n = len(L)
return maiorinteiro_aux(L, n)
São dados um conjunto de n discos com diferentes tamanhos e
três bases A, B e C.
O problema consiste em imprimir os passos necessários para transferir os discos da base A para a base B, usando a base C como auxiliar, nunca colocando discos maiores sobre menores.
Exemplo:
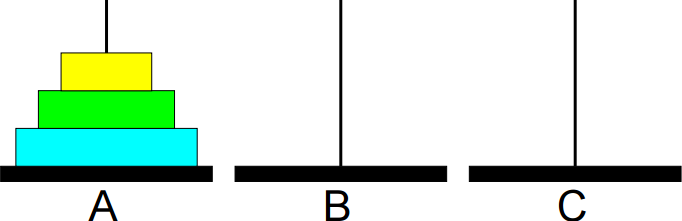
1º passo: Mover de A para B.
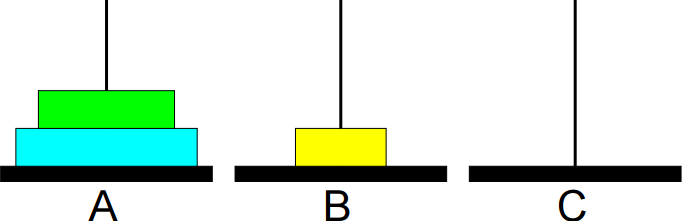
2º passo: Mover de A para C.
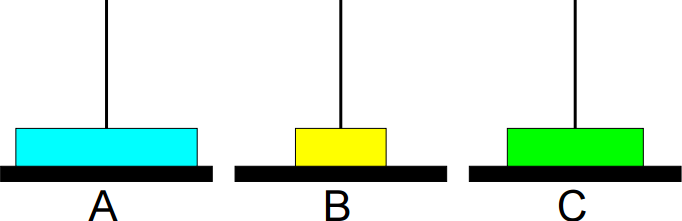
3º passo: Mover de B para C.
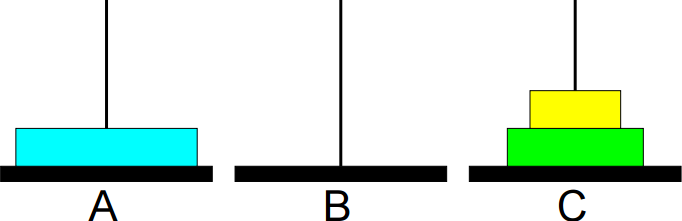
4º passo: Mover de A para B.
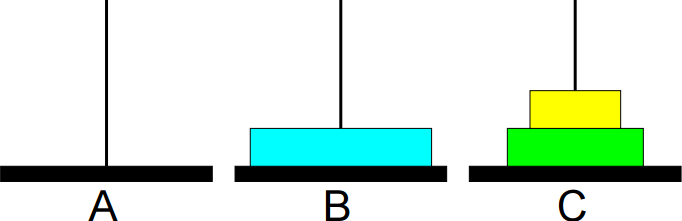
5º passo: Mover de C para A.
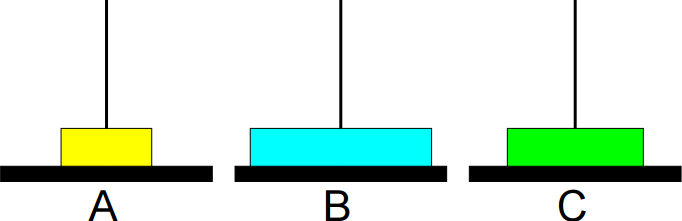
6º passo: Mover de C para B.
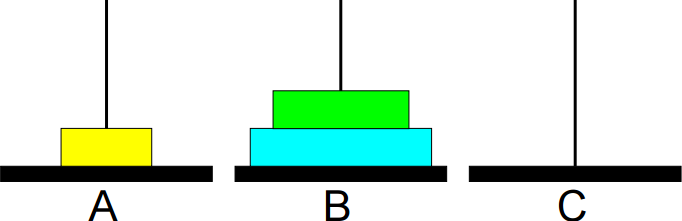
7º passo: Mover de A para B.
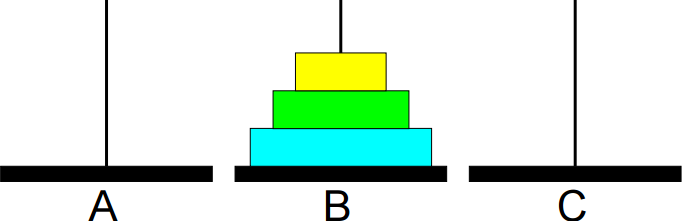
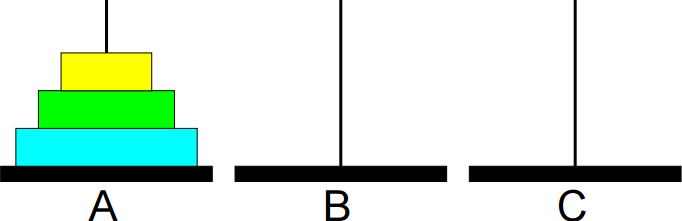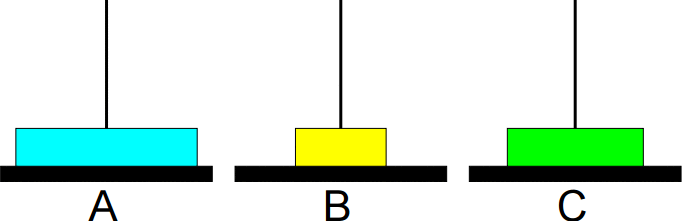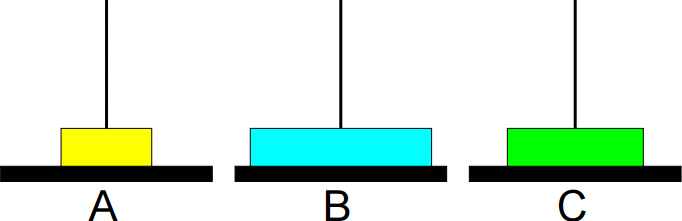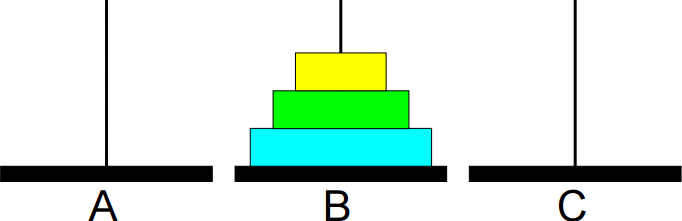
Animação da sequência completa de movimentos:
Solução:
def hanoi(n, orig, dest, aux):
if n == 1:
print("Mover de",orig,"para",dest)
else:
hanoi(n-1, orig, aux, dest)
print("Mover de",orig,"para",dest)
hanoi(n-1, aux, dest, orig)
def main():
n = int(input("Digite a quantidade de discos: "))
hanoi(n, "A", "B", "C")
main()
O número de movimentos necessários para mover n discos é 2n - 1.
n > 0 números inteiros,
faça uma função para ordenar os seus elementos em ordem crescente.
Solução 1:
Utilizaremos a seguinte função auxiliar
para realizar a troca entre os elementos da lista L
nos índices i e j:
def troca(L, i, j): tmp = L[i] #Guarda cópia de backup do valor L[i] em tmp. L[i] = L[j] L[j] = tmpA primeira solução apresentada utiliza a função auxiliar abaixo que devolve o índice do maior elemento da lista compreendido entre os índices de
0 a n-1.
def indice_maior(L, n):
imax = 0
for i in range(1,n):
if L[i] > L[imax]:
imax = i
return imax
No algoritmo abaixo, a cada passo o maior elemento da lista de n elementos
é encontrado, e colocado na sua posição final definitiva
de índice n-1 no final da lista.
O processo se repete para o trecho da lista remanescente,
composto pelos primeiros n-1 elementos ainda não ordenados
(do índice zero até n-2),
e assim por diante para subtrechos cada vez menores, até ter toda a lista ordenada.
Este algoritmo é conhecido como algoritmo de ordenação
por seleção simples.
def ordenacao_selecao(L):
"""Ordenação por seleção:
A cada passo o maior elemento da lista é
encontrado e colocado na sua posição
final definitiva. O processo se repete para o
trecho da lista remanescente."""
n = len(L)
for tam in range(n, 1, -1):
imax = indice_maior(L, tam)
troca(L, imax, tam-1)
No código acima, o laço controla em tam
o tamanho da porção
da lista a ser ordenada (elementos de
L[0] até L[tam-1]).
A chamada da função indice_maior
busca e armazena em imax o índice do maior elemento
presente no subtrecho do vetor a ser ordenado.
O elemento L[imax] é então
movido para a última posição
do subtrecho (L[tam-1]),
ocupando assim a sua posição definitiva.
Inicialmente, o subtrecho a ser ordenado
corresponde a toda a lista (elementos de
L[0] até L[n-1]).
A medida que os maiores valores são movidos
para o final da lista, temos a correspondente redução
do subtrecho remanescente a ser ordenado.
Solução 2:
O próximo algoritmo é conhecido como
bubble sort.
O laço mais interno percorre a lista
em j
comparando elementos consecutivos da lista (L[j] e
L[j+1]) e trocando a sua ordem sempre que
eles estiverem fora de ordem, isto é L[j] > L[j+1].
Após a primeira varredura, o maior elemento da lista
vai ocupar a última posição da lista,
ou seja sua posição final definitiva na lista ordenada.
A medida que os maiores valores são movidos
para o final da lista, temos a correspondente redução
do subtrecho remanescente a ser ordenado, até que
todo a lista esteja ordenada.
def ordenacao_bolha(L):
n = len(L)
for i in range(n-1, 0, -1):
for j in range(0,i):
if L[j] > L[j+1]:
troca(L, j, j+1)
Uma segunda versão do algoritmo bubble sort
é apresentada abaixo.
Essa variante possui um segundo critério de parada
do laço. Sempre que a lista é percorrida
no laço mais interno, sem que haja trocas de elementos,
podemos concluir que a lista já se encontra ordenada
e podemos interromper o processo.
def ordenacao_bolha(L):
n = len(L)
for i in range(n-1,0,-1):
houvetroca = False
for j in range(0,i):
if L[j] > L[j+1]:
troca(L, j, j+1)
houvetroca = True
if not houvetroca:
break
Solução 3:
Ordenação por inserção: Assume que uma parte da sequência já está ordenada, e insere mais um elemento no lugar apropriado.
def ordenacao_insercao(L):
n = len(L)
for i in range(0,n-1):
# Insere L[i+1] em L[0],...,L[i].
x = L[i+1]
j = i
while j >= 0 and L[j] > x:
L[j+1] = L[j]
j -= 1
L[j+1] = x
n > 0 valores inteiros, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
Solução 1:
Solução por busca exaustiva percorrendo a lista.
def pertence(x, L):
n = len(L)
i = 0
while i < n:
if L[i] == x:
return True
i += 1
return False
Solução 2:
Essa solução
adiciona na posição seguinte a do último elemento
o valor de x, conseguindo com isso a
simplificação do laço que passa agora a realizar
uma única comparação para cada iteração.
Essa técnica de busca é
conhecida como busca com sentinela.
# busca com sentinela
def pertence(x, L):
n = len(L)
i = 0
L.append(x) #adiciona x no final da lista
while L[i] != x:
i += 1
L.pop() #remove x do final da lista
if i == n:
return False
else:
return True
Solução 3:
Essa terceira solução se aplica somente a listas previamente ordenadas. A cada iteração, o valor procurado é comparado com o elemento na posição central da lista, eliminando metade do intervalo de busca. Essa solução é conhecida como algoritmo de busca binária.
# Busca binária:
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
while inic <= fim:
meio = (inic+fim)//2
if x == L[meio]:
return True
elif x > L[meio]:
inic = meio+1
else:
fim = meio-1
return False
Solução 4:
Essa solução apresenta o algoritmo de busca binária de modo recursivo.
# Busca binária recursiva:
def pertence_aux(x, L, inic, fim):
meio = (inic+fim)//2
if inic > fim:
return False
elif x == L[meio]:
return True
elif x > L[meio]:
return pertence_aux(x, L, meio+1, fim)
else:
return pertence_aux(x, L, inic, meio-1)
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
return pertence_aux(x, L, inic, fim)
L com n > 0 números inteiros no intervalo de 0 a 255
(isto é, 0 <= L[i] <= 255 para i = 0,.., n-1),
faça uma função para ordenar os seus elementos em ordem crescente.
Solução 1:
Explorando o fato de que os valores estão em um intervalo limitado de 0 a 255, podemo usar o algoritmo de ordenação do Counting Sort. Para isso vamos usar uma lista de contadores para cada valor de 0 a 255. Portanto, o algoritmo necessita de memória auxiliar.
def ordenacao_por_contagem(L):
n = len(L)
C = [0]*256 #Lista de contadores
for i in range(0,n):
C[L[i]] += 1
#Agora C[k] contém o número de elementos iguais a k.
i = 0
for k in range(0,256):
for c in range(0,C[k]):
L[i] = k
i += 1
Exemplo de função principal que chama as
funções anteriores.
def main():
L = [6,3,9,2,7,1,0,4,8,5]
ordenacao_insercao(L)
for i in range(0,n):
print(L[i], end=" ")
print()
x = int(input("Digite x: "))
if pertence(x, L):
print("Sim")
else:
print("Não")
main()