
Uma função é dita recursiva quando dentro dela é feita uma ou mais chamadas a ela mesma.
A ideia é dividir um problema original um subproblemas menores de mesma natureza (divisão) e depois combinar as soluções obtidas para gerar a solução do problema original de tamanho maior (conquista). Os subproblemas são resolvidos recursivamente do mesmo modo em função de instâncias menores, até se tornarem problemas triviais que são resolvidos de forma direta, interrompendo a recursão.
Solução 1:
Solução não recursiva.
def fatorial(n):
fat = 1
while n > 1:
fat *= n
n -= 1
return fat
Solução 2:
Solução recursiva: n! = n.(n-1)!

def fatorial(n):
if n == 0: #Caso trivial
return 1 #Solução direta
else:
return n*fatorial(n-1) #Chamada recursiva

Exemplo da sequência:
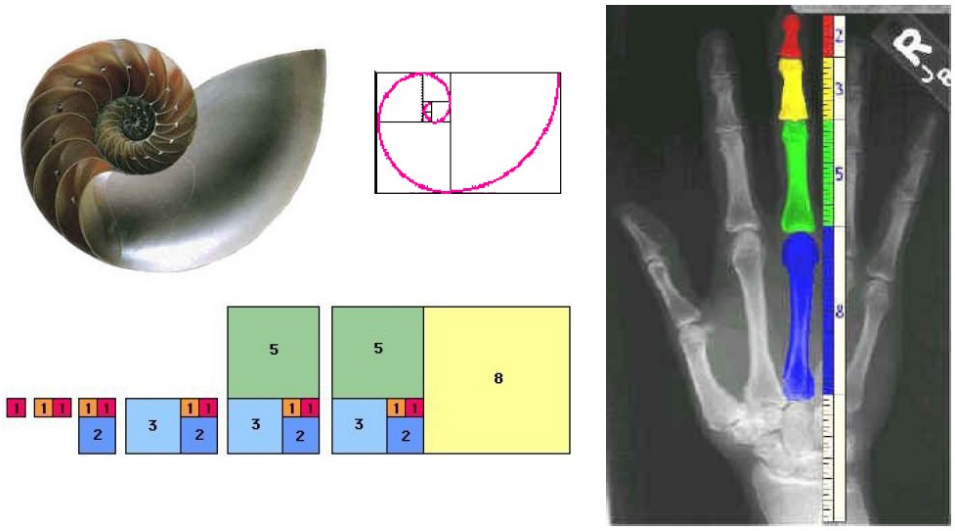
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...A ocorrência da sucessão de Fibonacci na natureza é tão frequente que é difícil acreditar que seja acidental (ex: flores, conchas, mão humana).
Solução 1:
Versão recursiva:
def fibo(n):
if n <= 1:
return n
else:
return fibo(n-1) + fibo(n-2)
Solução 2:
Versão não recursiva:
def fibo(n):
f0 = 0
f1 = 1
for k in range(1,n+1):
f2 = f0 + f1
f0 = f1
f1 = f2
return f0
Análise de eficiência das funções
Fibonacci calculando o número de operações
de soma S(n) realizadas:

Neste caso não faz sentido utilizar a versão recursiva.
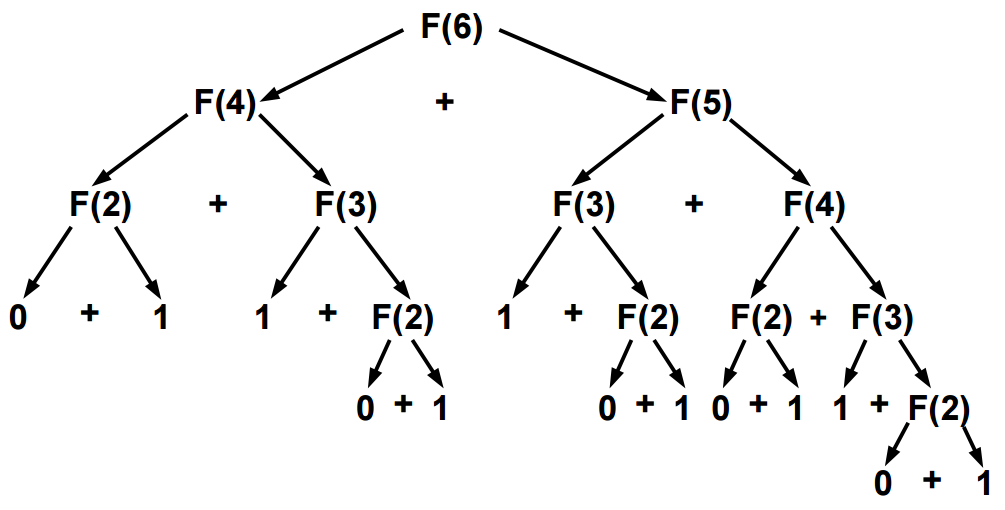
Árvore de Recorrência:
A solução recursiva é ineficiente, pois recalcula várias vezes a solução para valores intermediários:
Por exemplo, para F(6)=fibo(6) = 8, temos 2xF(4), 3xF(3), 5xF(2).
x elevado a n positivo.
Solução 1:
Solução não recursiva.
def potencia(x, n):
pot = 1.0
while n > 0:
pot *= x
n -= 1
return pot
Solução 2:
Solução recursiva: x^n = x . x^(n-1)
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0 #Solução direta
else:
return x*potencia(x, n-1) #Chamada recursiva
Solução 3:
Solução recursiva: x^n = x^(n/2). x^(n/2) = (x^(n/2))^2
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0
elif n%2 == 0: #Se n é par...
pot = potencia(x, n//2)
return pot*pot
else: #Se n é ímpar...
pot = potencia(x, n//2)
return pot*pot*x
Solução:
#Encontra o maior valor de uma lista com n elementos.
def maiorinteiro_aux(L, n):
if n==1: #Caso trivial
return L[0]
else:
m = maiorinteiro_aux(L, n-1)
if m > L[n-1]:
return m
else:
return L[n-1]
def maiorinteiro(L):
n = len(L)
return maiorinteiro_aux(L, n)
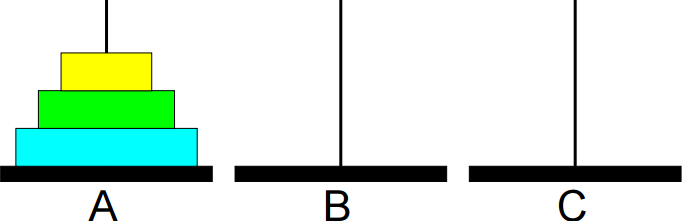
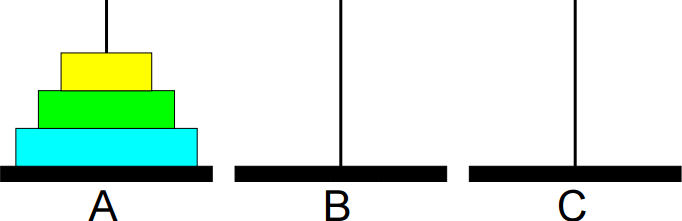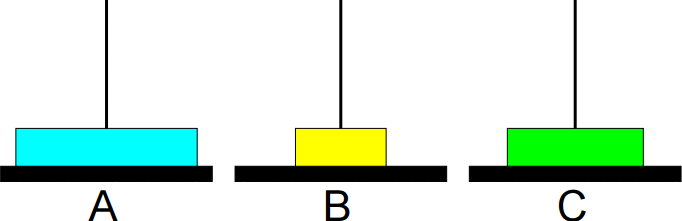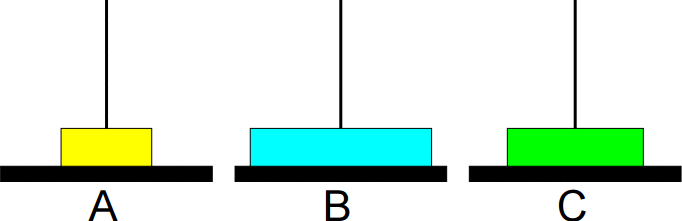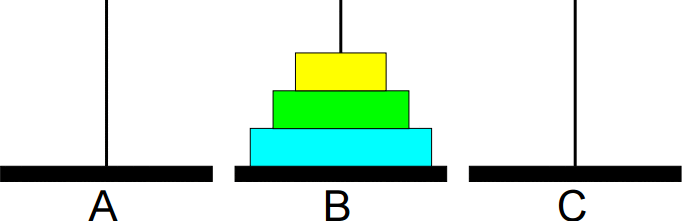
São dados um conjunto de n discos com diferentes tamanhos e
três bases A, B e C.
O problema consiste em imprimir os passos necessários para transferir os discos da base A para a base B, usando a base C como auxiliar, nunca colocando discos maiores sobre menores.
Exemplo:
1º passo: Mover de A para B.
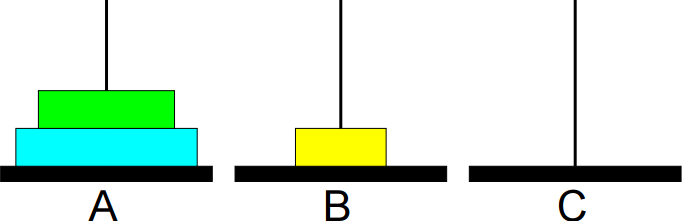
2º passo: Mover de A para C.
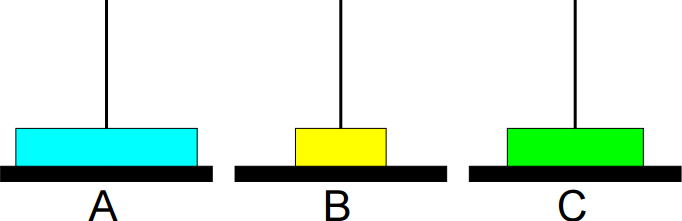
3º passo: Mover de B para C.
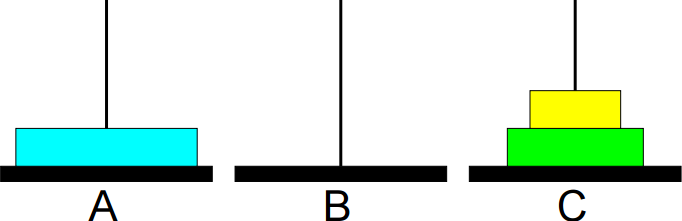
4º passo: Mover de A para B.
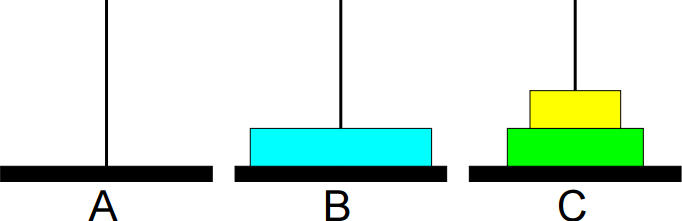
5º passo: Mover de C para A.
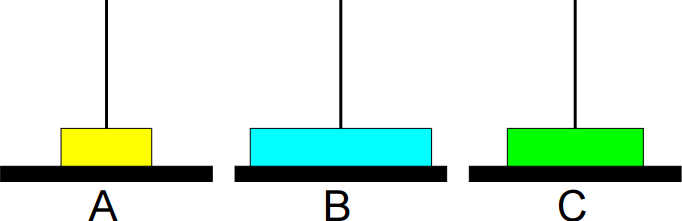
6º passo: Mover de C para B.
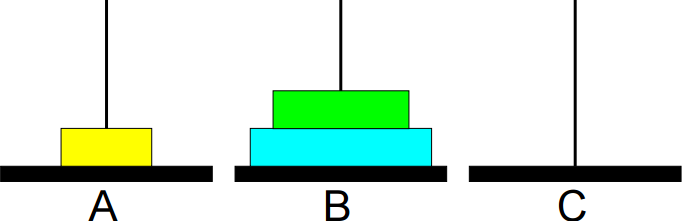
7º passo: Mover de A para B.
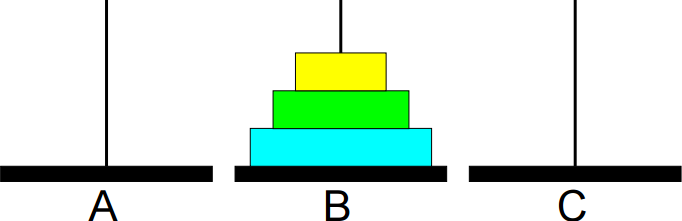
Animação da sequência completa de movimentos:
Solução:
def hanoi(n, orig, dest, aux):
if n == 1:
print("Mover de",orig,"para",dest)
else:
hanoi(n-1, orig, aux, dest)
print("Mover de",orig,"para",dest)
hanoi(n-1, aux, dest, orig)
def main():
n = int(input("Digite a quantidade de discos: "))
hanoi(n, "A", "B", "C")
main()
O número de movimentos necessários para mover n discos é 2n - 1.
n > 0 números inteiros,
faça uma função para ordenar os seus elementos em ordem crescente.
Solução 1:
Utilizaremos a seguinte função auxiliar
para realizar a troca entre os elementos da lista L
nos índices i e j:
def troca(L, i, j): tmp = L[i] #Guarda cópia de backup do valor L[i] em tmp. L[i] = L[j] L[j] = tmpA primeira solução apresentada utiliza a função auxiliar abaixo que devolve o índice do maior elemento da lista compreendido entre os índices de
0 a n-1.
def indice_maior(L, n):
imax = 0
for i in range(1,n):
if L[i] > L[imax]:
imax = i
return imax
No algoritmo abaixo, a cada passo o maior elemento da lista de n elementos
é encontrado, e colocado na sua posição final definitiva
de índice n-1 no final da lista.
O processo se repete para o trecho da lista remanescente,
composto pelos primeiros n-1 elementos ainda não ordenados
(do índice zero até n-2),
e assim por diante para subtrechos cada vez menores, até ter toda a lista ordenada.
Este algoritmo é conhecido como algoritmo de ordenação
por seleção simples.
def ordenacao_selecao(L):
"""Ordenação por seleção:
A cada passo o maior elemento da lista é
encontrado e colocado na sua posição
final definitiva. O processo se repete para o
trecho da lista remanescente."""
n = len(L)
for tam in range(n, 1, -1):
imax = indice_maior(L, tam)
troca(L, imax, tam-1)
No código acima, o laço controla em tam
o tamanho da porção
da lista a ser ordenada (elementos de
L[0] até L[tam-1]).
A chamada da função indice_maior
busca e armazena em imax o índice do maior elemento
presente no subtrecho do vetor a ser ordenado.
O elemento L[imax] é então
movido para a última posição
do subtrecho (L[tam-1]),
ocupando assim a sua posição definitiva.
Inicialmente, o subtrecho a ser ordenado
corresponde a toda a lista (elementos de
L[0] até L[n-1]).
A medida que os maiores valores são movidos
para o final da lista, temos a correspondente redução
do subtrecho remanescente a ser ordenado.
Solução 2:
O próximo algoritmo é conhecido como
bubble sort.
O laço mais interno percorre a lista
em j
comparando elementos consecutivos da lista (L[j] e
L[j+1]) e trocando a sua ordem sempre que
eles estiverem fora de ordem, isto é L[j] > L[j+1].
Após a primeira varredura, o maior elemento da lista
vai ocupar a última posição da lista,
ou seja sua posição final definitiva na lista ordenada.
A medida que os maiores valores são movidos
para o final da lista, temos a correspondente redução
do subtrecho remanescente a ser ordenado, até que
todo a lista esteja ordenada.
def ordenacao_bolha(L):
n = len(L)
for i in range(n-1, 0, -1):
for j in range(0,i):
if L[j] > L[j+1]:
troca(L, j, j+1)
Uma segunda versão do algoritmo bubble sort
é apresentada abaixo.
Essa variante possui um segundo critério de parada
do laço. Sempre que a lista é percorrida
no laço mais interno, sem que haja trocas de elementos,
podemos concluir que a lista já se encontra ordenada
e podemos interromper o processo.
def ordenacao_bolha(L):
n = len(L)
for i in range(n-1,0,-1):
houvetroca = False
for j in range(0,i):
if L[j] > L[j+1]:
troca(L, j, j+1)
houvetroca = True
if not houvetroca:
break
Solução 3:
Ordenação por inserção: Assume que uma parte da sequência já está ordenada, e insere mais um elemento no lugar apropriado.
def ordenacao_insercao(L):
n = len(L)
for i in range(0,n-1):
# Insere L[i+1] em L[0],...,L[i].
x = L[i+1]
j = i
while j >= 0 and L[j] > x:
L[j+1] = L[j]
j -= 1
L[j+1] = x
n > 0 valores inteiros, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
Solução 1:
Solução por busca exaustiva percorrendo a lista.
def pertence(x, L):
n = len(L)
i = 0
while i < n:
if L[i] == x:
return True
i += 1
return False
Solução 2:
Essa solução
adiciona na posição seguinte a do último elemento
o valor de x, conseguindo com isso a
simplificação do laço que passa agora a realizar
uma única comparação para cada iteração.
Essa técnica de busca é
conhecida como busca com sentinela.
# busca com sentinela
def pertence(x, L):
n = len(L)
i = 0
L.append(x) #adiciona x no final da lista
while L[i] != x:
i += 1
L.pop() #remove x do final da lista
if i == n:
return False
else:
return True
Solução 3:
Essa terceira solução se aplica somente a listas previamente ordenadas. A cada iteração, o valor procurado é comparado com o elemento na posição central da lista, eliminando metade do intervalo de busca. Essa solução é conhecida como algoritmo de busca binária.
# Busca binária:
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
while inic <= fim:
meio = (inic+fim)//2
if x == L[meio]:
return True
elif x > L[meio]:
inic = meio+1
else:
fim = meio-1
return False
Solução 4:
Essa solução apresenta o algoritmo de busca binária de modo recursivo.
# Busca binária recursiva:
def pertence_aux(x, L, inic, fim):
meio = (inic+fim)//2
if inic > fim:
return False
elif x == L[meio]:
return True
elif x > L[meio]:
return pertence_aux(x, L, meio+1, fim)
else:
return pertence_aux(x, L, inic, meio-1)
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
return pertence_aux(x, L, inic, fim)
L com n > 0 números inteiros no intervalo de 0 a 255
(isto é, 0 <= L[i] <= 255 para i = 0,.., n-1),
faça uma função para ordenar os seus elementos em ordem crescente.
Solução 1:
Explorando o fato de que os valores estão em um intervalo limitado de 0 a 255, podemo usar o algoritmo de ordenação do Counting Sort. Para isso vamos usar uma lista de contadores para cada valor de 0 a 255. Portanto, o algoritmo necessita de memória auxiliar.
def ordenacao_por_contagem(L):
n = len(L)
C = [0]*256 #Lista de contadores
for i in range(0,n):
C[L[i]] += 1
#Agora C[k] contém o número de elementos iguais a k.
i = 0
for k in range(0,256):
for c in range(0,C[k]):
L[i] = k
i += 1
Exemplo de função principal que chama as
funções anteriores.
def main():
L = [6,3,9,2,7,1,0,4,8,5]
ordenacao_insercao(L)
for i in range(0,n):
print(L[i], end=" ")
print()
x = int(input("Digite x: "))
if pertence(x, L):
print("Sim")
else:
print("Não")
main()
def ordenacao(M):
n = len(M)
for n in range(len(M),1,-1):
imax = 0
for i in range(1,n):
if M[i][0] > M[imax][0]:
imax = i
tmp = M[n-1]
M[n-1] = M[imax]
M[imax] = tmp
def main():
#Leitura do arquivo de entrada
arquivo = open("notas.csv", 'r')
matriz = []
for linha in arquivo:
l = linha.strip()
if len(l) > 0:
palavras = l.split(";")
matriz.append(palavras)
arquivo.close()
ordenacao(matriz)
#Gravação do arquivo de saída
arquivo = open("notas2.csv", 'w')
n = len(matriz)
m = len(matriz[0])
for i in range(n):
for j in range(m-1):
arquivo.write(matriz[i][j])
arquivo.write(";")
arquivo.write(matriz[i][m-1])
arquivo.write("\n")
arquivo.close()
main()
Inicialmente, usamos a função open() para
abrir o arquivo de nome notas.csv para leitura, tal como indicado pelo
valor 'r' (do inglês read) do segundo parâmetro de open("notas.csv", 'r'). O arquivo notas.csv deve estar no mesmo diretório do programa sendo executado,
caso contrário devemos indicar explicitamente o caminho completo (path) do arquivo.
Abaixo é mostrado um possível conteúdo do arquivo:
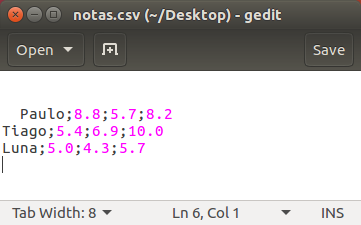
O comando for linha in arquivo: é então usado para
processar as linhas do arquivo, como se ele fosse uma lista de strings contendo as linhas do arquivo. Usamos o método strip() para eliminar o '\n' e demais caracteres considerados "brancos" (como o espaço e o tab) no início e final das linhas.
Adicionamos então na matriz as linhas não vazias do aquivo, como uma lista de palavras separadas por ; utilizando o método split(";").
Usamos então close para fechar o arquivo.
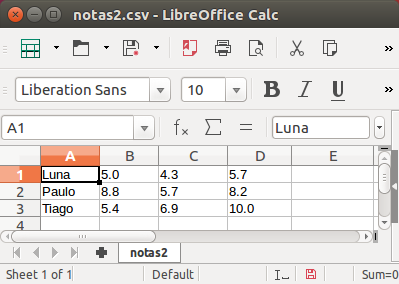
Para o exemplo fornecido, a seguinte matriz é obtida:
[['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0'], ['Luna', '5.0', '4.3', '5.7']]
A matriz é então ordenada pelo seu primeiro campo pela função ordenacao(). No exemplo, temos a seguinte matriz ordenada:
[['Luna', '5.0', '4.3', '5.7'], ['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0']]
A matriz ordenada é então gravada no disco. Para isso,
abrimos o arquivo de saída notas2.csv no modo gravação,
tal como indicado pelo valor 'w' (do inglês write) do segundo parâmetro
do comando open("notas2.csv", 'w').
O arquivo notas2.csv é gerado no mesmo diretório do programa sendo executado,
caso contrário devemos incluir todo o caminho (path) no seu nome.
Os elementos da matriz são gravados no disco usando
o método write(). Dado que o comando write()
não inclui automaticamente o caracter de quebra de linha,
devemos usar o "\n" explicitamente quando necessário.
Para o exemplo fornecido, temos o seguinte arquivo de saída:
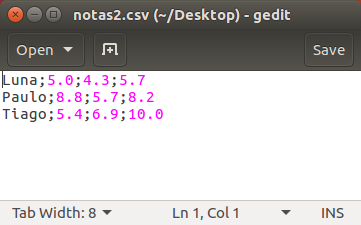
Arquivos no formato CSV são reconhecidos pelo OpenOffice/LibreOffice e programas similares. Abaixo mostramos o arquivo gerado sendo aberto no LibreOffice:
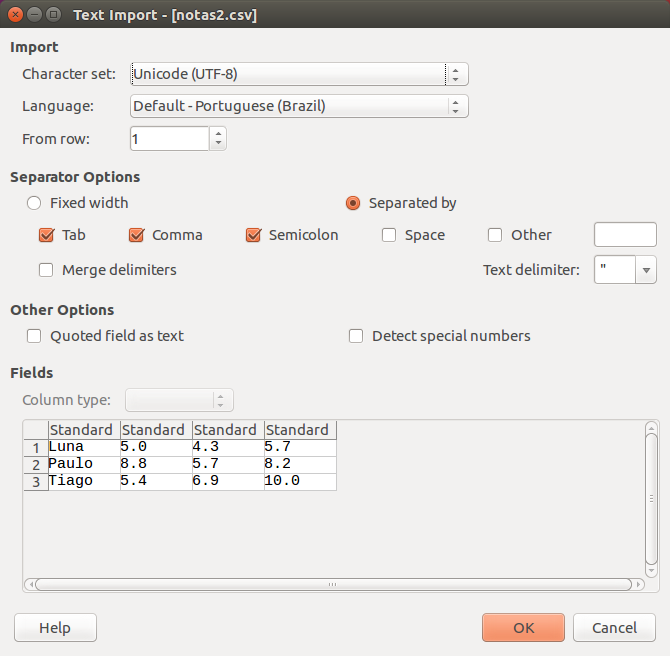
n>0, faça uma
função molduras_concentricas(n, v1, v2) que gera
uma matriz quadrada nxn preenchida
com um padrão de molduras concêntricas, alternando entre
dois valores fornecidos v1 e v2 como nos exemplos.
Para n=5, v1=0, v2=1:
[[0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 0, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0]]
Para n=7, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1]]
Para n=15, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
Solução:
#Cria matriz com m linhas e n colunas
def cria_matriz(m, n, valor):
M = []
for i in range(m):
linha = []
for j in range(n):
linha.append(valor)
M.append(linha)
return M
def molduras_concentricas(n, v1, v2):
M = cria_matriz(n, n, 0)
for i in range(n):
for j in range(n):
#dh = distancia horizontal ao centro
dh = n//2 - j
if dh < 0:
dh = -dh
#dv = distancia vertical ao centro
dv = n//2 - i
if dv < 0:
dv = -dv
if dh > dv:
if dh % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
else:
if dv % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
return M
def grava_PGM(M):
arquivo = open("fig01.pgm", 'w')
arquivo.write("P2\n")
m = len(M)
n = len(M[0])
arquivo.write("%d %d\n"%(n,m))
arquivo.write("255\n")
for i in range(m):
for j in range(n):
arquivo.write(" %3d"%(M[i][j]))
arquivo.write("\n")
arquivo.close()
def main():
n = int(input("Digite n: "))
M = molduras_concentricas(n, 0, 255)
grava_PGM(M)
main()
Invertendo o conteúdo das variáveis v1 e v2, obtemos uma imagem com o brilho invertido. Podemos gerar a gif animada abaixo, gravando essa segunda imagem em um arquivo fig02.pgm e usando o conversor de imagens do ImageMagick, executando no terminal o comando: convert -delay 10 *.pgm out.gif

A gif animada acima foi gerada usando n=101.
Que modificação você poderia fazer no código acima para obter molduras mais grossas como na figura abaixo?

Vamos usar a seguinte função auxiliar para criar uma matriz,
onde m é o número de linhas,
n é o número de colunas e
val é o valor inicial de preenchimento dos elementos da matriz.
def cria_matriz(m, n, val):
matriz = []
for i in range(m):
linha = []
for j in range(n):
linha.append(val)
matriz.append(linha)
return matriz
Para visualizar os resultados, vamos usar
a função abaixo que grava uma matriz
como uma imagem no formato PGM,
onde o valor zero indica o preto e o valor 255 indica o branco.
def grava_PGM(matriz, nomearquivo):
arquivo = open(nomearquivo, "w")
arquivo.write("P2\n")
m = len(matriz)
n = len(matriz[0])
arquivo.write("%d %d\n"%(n,m))
arquivo.write("255\n")
for i in range(m):
for j in range(n):
arquivo.write(" %3d"%(matriz[i][j]))
arquivo.write("\n")
arquivo.close()
(x1, y1) e (x2, y2) das extremidades
de um segmento de reta e uma matriz representando uma imagem em tons de cinza, faça uma função recursiva que desenha o segmento de reta na imagem com um valor de intensidade fornecido.
Solução:
Na solução abaixo,
o problema original é decomposto em dois subproblemas
de mesma natureza, dividindo o segmento ao meio
em dois segmentos menores.
A cada passo as coordenadas do ponto médio (xm, ym)
são calculadas e duas chamadas recursivas são realizadas.
A parada da recursão acontece quando
o problema se torna simples, envolvendo dois pontos vizinhos ou iguais.
Neste caso a solução trivial corresponde a pintar os dois pontos.
Note, no entanto, que somente podemos acessar posições da matriz
utilizando índices inteiros, caso contrário, teremos o seguinte erro:
list indices must be integers or slices, not float.
O arredondamento das coordenadas é obtido somando 0.5 antes de truncar os números (desprezar a parte fracionária) com o comando int().
def desenha_reta(matriz, x1,y1, x2,y2, val):
if abs(x2-x1) <= 1 and abs(y2-y1) <= 1:
matriz[int(y1+0.5)][int(x1+0.5)] = val
matriz[int(y2+0.5)][int(x2+0.5)] = val
else:
xm = (x1+x2)/2
ym = (y1+y2)/2
desenha_reta(matriz, x1,y1, xm,ym, val)
desenha_reta(matriz, xm,ym, x2,y2, val)
Exemplo de função principal que chama as
funções anteriores.
def main():
M = cria_matriz(240, 320, 0)
desenha_reta(M, 20,15, 300,210, 255)
grava_PGM(M, "reta.pgm")
main()
A figura abaixo apresenta o resultado da execução do programa acima.

OBS: Um algoritmo mais adequado para o desenho de linhas, em dispositivos matriciais, corresponde ao algoritmo de Bresenham.
O objetivo deste exercício é fazer um programa em Python, usando funções recursivas, para gerar imagens (no formato PGM) com os desenhos de um fractal conhecido como Tapete de Sierpinski.
A construção do Tapete de Sierpinski parte de um quadrado, que é subdividido em nove partes. A parte central é removida, de modo que sobram então oito pequenos quadrados. Para cada um deles, é aplicado o mesmo processo de divisão em nove partes, retirando a parte central, e assim sucessivamente. Este processo pode ser repetido infinitamente, mas no contexto de imagens a repetição é feita até atingir um número máximo de iterações.
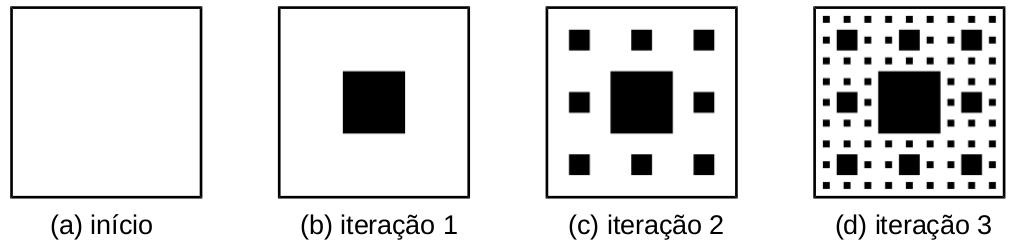
Solução:
A função tapete_sierpinski(n, niveis)
gera uma imagem quadrada nxn do tapete de Sierpinski,
onde niveis é o número máximo de iterações e o quadrado inicial do tapete corresponde a toda a imagem.
A função recursiva tapete_sierpinski_aux(matriz, x1,y1, x2,y2, niveis) realiza a divisão do quadrado, compreendido entre as coordenadas
(x1,y1) e (x2,y2), em nove partes e pinta a parte central de preto, conforme a ilustração abaixo.
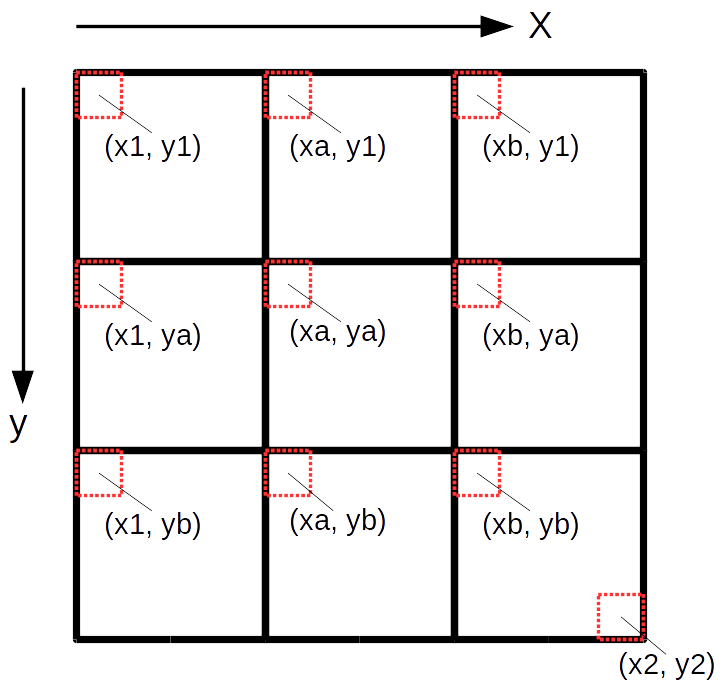
def tapete_sierpinski_aux(matriz, x1,y1, x2,y2, niveis):
if niveis > 0:
tam = x2-x1+1
xa = x1 + tam//3
xb = xa + tam//3
ya = y1 + tam//3
yb = ya + tam//3
tapete_sierpinski_aux(matriz, x1,y1, xa-1,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, x1,ya, xa-1,yb-1, niveis-1)
tapete_sierpinski_aux(matriz, x1,yb, xa-1,y2, niveis-1)
tapete_sierpinski_aux(matriz, xa,y1, xb-1,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, xa,yb, xb-1,y2, niveis-1)
tapete_sierpinski_aux(matriz, xb,y1, x2,ya-1, niveis-1)
tapete_sierpinski_aux(matriz, xb,ya, x2,yb-1, niveis-1)
tapete_sierpinski_aux(matriz, xb,yb, x2,y2, niveis-1)
for i in range(ya,yb):
for j in range(xa,xb):
matriz[i][j] = 0
def tapete_sierpinski(n, niveis):
M = cria_matriz(n, n, 255)
tapete_sierpinski_aux(M, 0,0, n-1,n-1, niveis)
return M
Exemplo de função principal que chama as
funções anteriores, considerando uma imagem quadrada nxn,
onde n é uma potência de três (ex: 3^6 = 729) e
o nome do arquivo de saída é tapete.pgm.
def main():
n = 3**6
T = tapete_sierpinski(n, 5)
grava_PGM(T, "tapete.pgm")
main()
A figura abaixo apresenta o resultado da execução do programa acima.
