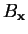Next: Mínima Distância ao(s) Protótipo(s)
Up: Regra dos K vizinhos
Previous: distância Euclidiana
Contents
Index
distância de Mahalanobis
A distância de Mahalanobis entre um padrão 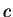 e o protótipo
e o protótipo 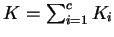 de uma classe é definida por:
de uma classe é definida por:
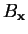 |
(2.17) |
em que 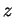 é a matriz de covariância dos padrões da classe de
é a matriz de covariância dos padrões da classe de 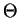 . 2.2
Tomando-se
. 2.2
Tomando-se 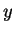 no classificador de K vizinhos mais próximos, obtém-se o classificador de vizinho mais próximo (1NN). Esse classificador é muito comum em aplicações de reconhecimento de faces após a extração de características usando PCA. Normalmente, a regra de classificação por vizinho mais próximo acarreta numa taxa de erro maior do que a da regra de decisão de Bayes. Porém existe um teorema que diz que, supondo-se que haja infinitos de padrões de treinamento, a taxa de erro com esse classificador não ultrapassa (sendo em geral menor que) o dobro da taxa de erro com o classificador de Bayes (ver demonstração [Kohn, 1998] e [Theodoridis and Koutroumbas, 1999]).
O classificador KNN pode ser descrito formalmente utilizando o classificador de Bayes com mínima taxa de erro. A desigualdade contida na equação 2.13 equivale a
no classificador de K vizinhos mais próximos, obtém-se o classificador de vizinho mais próximo (1NN). Esse classificador é muito comum em aplicações de reconhecimento de faces após a extração de características usando PCA. Normalmente, a regra de classificação por vizinho mais próximo acarreta numa taxa de erro maior do que a da regra de decisão de Bayes. Porém existe um teorema que diz que, supondo-se que haja infinitos de padrões de treinamento, a taxa de erro com esse classificador não ultrapassa (sendo em geral menor que) o dobro da taxa de erro com o classificador de Bayes (ver demonstração [Kohn, 1998] e [Theodoridis and Koutroumbas, 1999]).
O classificador KNN pode ser descrito formalmente utilizando o classificador de Bayes com mínima taxa de erro. A desigualdade contida na equação 2.13 equivale a
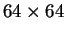 , contando que
, contando que
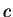 . Para estimar
. Para estimar 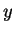 a partir dos dados, basta tomar
a partir dos dados, basta tomar 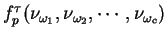 , em que
, em que 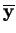 é o número total de amostras e
é o número total de amostras e 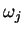 é o número de amostras na classe
é o número de amostras na classe 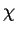 . Para se estimar
. Para se estimar
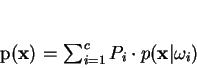 , pode-se tomar um volume
, pode-se tomar um volume 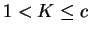 , centrado em
, centrado em 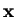 e contar-se quantas amostras há em seu interior. Dessa forma, a regra de decisão de Bayes fica:
e contar-se quantas amostras há em seu interior. Dessa forma, a regra de decisão de Bayes fica:
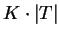 |
(2.18) |
em que se supõe que volume 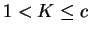 abarca exatamente K amostras indistintamente das classes envolvidas, com
abarca exatamente K amostras indistintamente das classes envolvidas, com
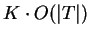 .
Simplificando,
.
Simplificando,
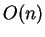 |
(2.19) |
A principal vantagem desse método é que ele cria uma superfície de decisão que se adapta à forma de distribuição dos dados de treinamento de maneira detalhada, possibilitando a obtenção de boas taxas de acerto quando o conjunto de treinamento é grande ou representativo.
O objetivo de se utilizar 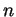 é reduzir a ocorrência de erros causados por ruídos nos padrões de treinamento. Por exemplo, um padrão de treinamento
é reduzir a ocorrência de erros causados por ruídos nos padrões de treinamento. Por exemplo, um padrão de treinamento 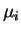 da classe
da classe 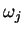 que se encontra em uma região do espaço de características povoada por padrões de treinamento da classe
que se encontra em uma região do espaço de características povoada por padrões de treinamento da classe 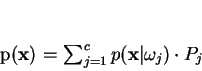 devido à ação de ruídos não prejudicará o desempenho do classificador, pois a verificação de seus vizinhos fará com que um padrão de teste que se localize próximo a
devido à ação de ruídos não prejudicará o desempenho do classificador, pois a verificação de seus vizinhos fará com que um padrão de teste que se localize próximo a
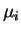 seja classificado como um padrão da classe
seja classificado como um padrão da classe 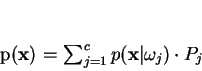 .
Porém, o uso de valores grandes em
.
Porém, o uso de valores grandes em 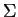 pode reduzir a qualidade dos resultados de classificação quando a distribuição das classes possui muitas sobreposições.
Assim, deve-se ter preferência ao classificador KNN sobre o 1NN quando se dispõe de um conjunto de treinamento
pode reduzir a qualidade dos resultados de classificação quando a distribuição das classes possui muitas sobreposições.
Assim, deve-se ter preferência ao classificador KNN sobre o 1NN quando se dispõe de um conjunto de treinamento 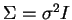 com muitos exemplos e quando esse conjunto contiver amostras com classificação errada.
Por essas razões, a escolha do número de vizinhos a serem utilizados (K) torna-se um ponto crítico do classificador KNN. Não há uma estratégia definitiva para realizar essa escolha para um caso prático, sendo recomendada a estratégia de tentativa e erro. Porém, pesquisas recentes [Theodoridis and Koutroumbas, 1999] sugerem que, para
com muitos exemplos e quando esse conjunto contiver amostras com classificação errada.
Por essas razões, a escolha do número de vizinhos a serem utilizados (K) torna-se um ponto crítico do classificador KNN. Não há uma estratégia definitiva para realizar essa escolha para um caso prático, sendo recomendada a estratégia de tentativa e erro. Porém, pesquisas recentes [Theodoridis and Koutroumbas, 1999] sugerem que, para
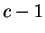 , quando
, quando
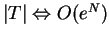 , o desempenho do classificador KNN tende a ser ótimo. Entretanto, para conjunto de treinamento numerosos, é esperado que o classificador 3NN (KNN para K=3) permita a obtenção de um desempenho muito próximo do classificador Bayesiano.
Um fato óbvio é que a escolha de
, o desempenho do classificador KNN tende a ser ótimo. Entretanto, para conjunto de treinamento numerosos, é esperado que o classificador 3NN (KNN para K=3) permita a obtenção de um desempenho muito próximo do classificador Bayesiano.
Um fato óbvio é que a escolha de 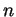 (principalmente
(principalmente 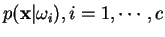 , sendo
, sendo 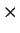 o número de classes) pode causar problemas de indecisão quando ocorrem empates, ou seja, quando o número de vizinhos mais próximos pertencente a classes diferentes é igual.
A principal desvantagem dos classificadores K-NN está em sua complexidade na fase de testes. Isso deve-se ao fato de que, caso seja feita uma busca em ``força-bruta'' (sem ordenação) pelos vizinhos mais próximos, para cada padrão de teste é necessário realizar
o número de classes) pode causar problemas de indecisão quando ocorrem empates, ou seja, quando o número de vizinhos mais próximos pertencente a classes diferentes é igual.
A principal desvantagem dos classificadores K-NN está em sua complexidade na fase de testes. Isso deve-se ao fato de que, caso seja feita uma busca em ``força-bruta'' (sem ordenação) pelos vizinhos mais próximos, para cada padrão de teste é necessário realizar 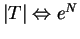 medições de distância, ou seja, a quantidade de operações necessárias é da ordem de
medições de distância, ou seja, a quantidade de operações necessárias é da ordem de
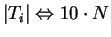 , sendo que
, sendo que 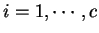 denota a ordem de
denota a ordem de 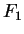 cálculos [Theodoridis and Koutroumbas, 1999,Cormen et al., 1990].
cálculos [Theodoridis and Koutroumbas, 1999,Cormen et al., 1990].





Next: Mínima Distância ao(s) Protótipo(s)
Up: Regra dos K vizinhos
Previous: distância Euclidiana
Contents
Index
Teofilo Emidio de Campos
2001-08-29