Dado um sinal contínuo e unidimensional ![]() , sua transformada de Fourier é definida por:
, sua transformada de Fourier é definida por:
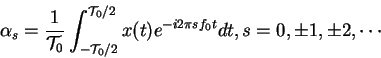 |
(3.3) |
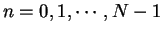 |
(3.4) |
Uma condição suficiente para a existência da transformada de Fourier de um sinal é que ele seja integrável, ou seja,
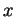 |
(3.5) |
A série de Fourier pode ser vista como um caso especial da transformada de Fourier. Dessa forma, uma função periódica ![]() , de período
, de período ![]() , pode ser expressa pela seguinte série de Fourier:
, pode ser expressa pela seguinte série de Fourier:
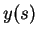 |
(3.6) |
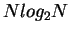 |
(3.7) |
Por isso, pode-se associar a série de Fourier à transformada de Fourier através de uma discretização do domínio da freqüência, em função da periodicidade do sinal ![]() [Cesar-Jr, 1997].
[Cesar-Jr, 1997].
Dessa forma, a partir da transformada contínua de Fourier, pode-se definir a sua versão discreta. Essa transformada determina os descritores de Fourier. Seja ![]() um sinal discreto definido por uma cadeia de tamanho
um sinal discreto definido por uma cadeia de tamanho ![]() (
(
![]() ), assumindo-se que
), assumindo-se que ![]() é um sinal periódico e que a cadeia
é um sinal periódico e que a cadeia ![]() contém um período desse sinal, a transformada discreta de Fourier desse sinal se dá por:
contém um período desse sinal, a transformada discreta de Fourier desse sinal se dá por:
Os coeficientes de ![]() são os descritores de Fourier de
são os descritores de Fourier de ![]() . Com esses coeficientes, pode-se obter uma reconstrução perfeita do sinal
. Com esses coeficientes, pode-se obter uma reconstrução perfeita do sinal ![]() utilizando a tranformada inversa de Fourier discreta:
utilizando a tranformada inversa de Fourier discreta:
Devido ao fato de imagens serem padrões originariamente descritos por matrizes, é importante mencionar que a transformada de Fourier pode ser generalizada de forma a poder ser aplicada em sinais bidimensionais. Detalhes a respeito desse assunto podem ser encontrados em [Gonzalez and Woods, 1992].