Preliminares

A maioria dos métodos determinísticos de solução única são baseados em buscas. Dentre eles, a maioria possui duas abordagens: para frente ( botton-up) e para trás ( top-down). Na abordagem para frente, inicia-se com um conjunto de avaliação (temporário) vazio e, conforme o algoritmo é executado, são inseridas características nesse conjunto, até que esse fique com tamanho $m$. Já na abordagem para trás, inicia-se com um conjunto de avaliação contendo todas as características disponíveis e, nas iterações do algoritmo, são excluídas características até que esse conjunto fique com o tamanho $m$. Em geral, podem-se dizer que os métodos para frente são mais rápidos que seus equivalentes para trás, pois o custo de medição da função critério em conjuntos de características grandes é maior que o custo em conjuntos pequenos [Jain and Zongker, 1997]. Porém, quando o valor de $m$ é próximo de $N$, deve-se dar preferência à utilização dos métodos para trás.

Abaixo apresentamos as definições utilizadas nos trabalhos de [Pudil et al., 1994] e [Somol et al., 1999] na descrição dos métodos de busca seqüenciais.

Seja $\calX_k = \{x_i : 1 \leq i \leq k, x_i \in \calY\}$ um subconjunto de $k$ características do conjunto $\calY = \{y_i: 1 \leq i \leq N\}$ das $N$ características disponíveis, o valor $J(y_i)$ da função critério de seleção de características, quando somente a $i$-ésima característica $y_i$, $i = 1, 2, \cdots, N$ for utilizada, é chamado de significância individual $\calS_0(y_i)$ da característica.

A significância $\calS_{k-1}(x_j)$ da característica $x_j$, $j = 1, 2, \cdots, k$ no conjunto $\calX_k$ é definida por

$$\calS_{k-1}(x_j) = J(\calX_k) - J(\calX_k - x_j)$$ (3.22)

A significância $\calS_{k+1}(f_j)$ da característica $f_j$ do conjunto $\calY - \calX_k$, tal que $\calY - \calX_k = \{f_i : i = k +1, k + 2, \cdots, N, f_i \in \calY, f_i \neq x_l, \forall x_l \in \calX_k\}$, em relação ao conjunto $\calX_k$, é definida por

$$\calS_{k+1}(f_i) = J(\calX_k + f_j) - J(\calX_k).$$ (3.23)

Nota: para $k=0$, o termo significância de uma característica no conjunto coincide com o termo significância individual.

Dizemos que a característica $x_j$ do conjunto $\calX_k$ é:

1. a característica mais significante (melhor) do conjunto $\calX_k$ se
   

   $$\calS_{k-1}(x_j) = \max_{1 \leq i \leq k} \calS_{k-1}(x_i) \... ...w J(\calX_k - x_j) = \min_{1 \leq i \leq k} J(\calX_k - x_i),$$ (3.24)

   
   

2. a característica menos significante (pior) do conjunto $\calX_k$ se
   

   $$\calS_{k-1}(x_j) = \min_{1 \leq i \leq k} \calS_{k-1}(x_i) \... ...w J(\calX_k - x_j) = \max_{1 \leq i \leq k} J(\calX_k - x_i).$$ (3.25)

   
   

Dizemos que a característica $f_j$ do conjunto $\calY - \calX_k$ é:

1. a característica mais significante (melhor) em relação ao conjunto $\calX_k$ se
   

   $$\calS_{k+1}(f_j) = \max_{k+1 \leq i \leq N} \calS_{k+1}(f_i)... ... J(\calX_k + f_j) = \max_{k+1 \leq i \leq N} J(\calX_k + f_i),$$ (3.26)

   
   

2. a característica menos significante (pior) em relação ao conjunto $\calX_k$ se
   

   $$\calS_{k+1}(f_j) = \min_{k+1 \leq i \leq N} \calS_{k+1}(f_i)... ... J(\calX_k - f_j) = \min_{k+1 \leq i \leq N} J(\calX_k + x_i).$$ (3.27)

   
   

Seja $\calT_o$ genericamente uma tupla de $o$ características, o valor da função critério $J(\calT_o)$, quando somente as características $t_i, i=1, 2, \cdots, o, t_i \in \calT_o$ forem utilizadas, será chamado significância individual $\calS_0(T_o)$ da $o$-tupla de características.

A significância $\calS_{k-o}(\calT_o)$ da $o$-tupla de características $\calT_o = \{t_i: 1 \leq i \leq o, t_i \in \calX_k\}$ no conjunto $\calX_k$ é definida por

$$\calS_{k-o}(\calT_o) = J(\calX_k) - J(\calX_k - \calT_o).$$ (3.28)

A significância $\calS_{k+o}(\calU_o)$ da $o$-tupla de características $\calU_o = \{u_i: 1 \leq i \leq o$, $u_i \in \calY - \calX_k\}$ no conjunto $\calY - \calX_k$ em relação ao conjunto $\calX_k$ é definida por

$$\calS_{k+o}(\calU_o) = J(\calX_k \bigcup \calU_o) - J(\calX_k).$$ (3.29)

Denotamos por $\calT_o^i$ a $i$-ésima tupla contida no conjunto de todas as $\Theta = (^k_o)$ $o$-tuplas possíveis de $\calX_k, 1 \leq i \leq \Theta$. Pode-se dizer que a $o$-tupla de características $\calT_o^i$ do conjunto $\calX_k$ é:

1. a $o$-tupla de características mais significante (melhor) do conjunto $\calX_k$ se
   

   $$\calS_{k-o}(\calT_o^n) = \max_{1 \leq i \leq \Theta} \calS_{... ...\calT_o^n) = \min_{1 \leq i \leq \phi} J(\calX_k - \calT_o^i);$$ (3.30)

   
   

2. a $o$-tupla de características menos significante (pior) do conjunto $\calX_k$ se
   

   $$\calS_{k-o}(\calT_o^n) = \min_{1 \leq i \leq \Theta} \calS_{... ...alT_o^n) = \max_{1 \leq i \leq \Theta} J(\calX_k - \calT_o^i).$$ (3.31)

   
   

Dizemos que a $o$-tupla de características $\calU_o$ do conjunto $\calY - \calX_k$ é:

1. a $o$-tupla de características mais significante (melhor) em relação ao conjunto $\calX_k$ se
   

   $$\calS_{k+o}(\calU_o^r) = \max_{1 \leq i \leq \Psi} \calS_{k+... ...o^r) = \max_{1 \leq i \leq \Psi} J(\calX_k \bigcup \calU_o^i),$$ (3.32)

   
   
   em que $\Psi = (^{N-k}_o)$ é o número de todas as $o$-tuplas possíveis de $\calY - \calX_k$;

2. a $o$-tupla de características menos significante (pior) em relação ao conjunto $\calX_k$ se
   

   $$\calS_{k+o}(\calU_o^r) = \min_{1 \leq i \leq \Psi} \calS_{k+... ...o^r) = \min_{1 \leq i \leq \Psi} J(\calX_k \bigcup \calU_o^i).$$ (3.33)

   
   

Nota: para $o = 1$, todos os termos relacionados com o significado de $o$-tuplas de características coincidem com os termos relacionados com a significância individual de uma característica.

A seguir apresentamos a descrição dos principais métodos de seleção de características determinísticos de solução única.

Melhores Características Individuais

O método de seleção de características pelas melhores caracteríticas individuais consiste na avaliação de todas as características tomadas individualmente e seleção das $m$ melhores. O algoritmo abaixo detalha esse método. Note que, para fim de facilitar a exposição, o parâmetro $k$ dos conjuntos $X$ foi omitido nesse e nos próximos algoritmos, pois o valor de $k$ varia conforme a execução dos algoritmos e os algoritmos podem ser chamados com conjuntos de diferentes tamanhos.

Como as características são avaliadas individualmente, esse método não é classificado nem como para frente, nem como para trás. Trata-se de um método bastante intuitivo e computacionalmente simples, mas que não garante que o melhor subconjunto seja determinado, pois algumas características podem ser boas tomadas individualmente, mas podem formar um conjunto ruim quando associadas entre si. Outros detalhes sobre esse método encontram-se em [Jain and Zongker, 1997,Theodoridis and Koutroumbas, 1999]

Busca Seqüencial para Frente (SFS)

O método de busca seqüencial para frente, como o próprio nome diz, é um método botton-up. Dado um conjunto de características já selecionadas (inicialmente nulo), a cada iteração é seleciona a característica que, unida ao conjunto determinado pela iteração anterior, produz o melhor resultado da função critério. Essa característica é adicionada ao conjunto de características anterior e uma nova iteração é realizada. São realizadas $m$ iterações. O algoritmo a seguir detalha esse processo, devem-se assumir que inicialmente $\calX \leftarrow \emptyset$.

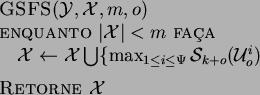
Observa-se que a instrução $\calX \leftarrow \emptyset$ não foi incluída no algoritmo da função SFS($\cdot$), pois essa função será utilizada posteriormente para conjuntos não vazios. Isso repetir-se-á na função SBS($\cdot$) a seguir.

A desvantagem desse método é que, uma vez que uma característica tenha sido selecionada, ela não pode ser descartada do subconjunto ótimo, o que pode proporcionar o chamado efeito nesting. O efeito nesting ocorre quando o subconjunto ótimo não contém elementos do conjunto já selecionado, o que impossibilita que seja obtido o conjunto de características ótimo.

A principal vantagem da busca seqüencial para frente é o custo computacional quando se deseja obter conjuntos pequenos em relação ao total de caracteríscias. Outros detalhes a respeito desses métodos podem ser encontrados em [Jain and Zongker, 1997,Theodoridis and Koutroumbas, 1999].

Busca Seqüencial para Trás (SBS)

O algoritmo de busca seqüencial para trás é uma versão top-down do algoritmo anterior. A diferença entre SBS e SFS é que o SBS é iniciado com o conjunto de características completo (contendo todas as $N$ características) e vai eliminando as menos importantes, ou seja, as que menos alteram a função critério quando são eliminadas. O algoritmo a seguir detalha esse processo, devem-se assumir que inicialmente $\calX \leftarrow \calY$.

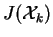
Assim como o método de busca seqüencial para frente, a desvantagem desse método é que, uma vez eliminada uma característica, ela não retornará ao subconjunto ótimo novamente. Como conseqüência, também pode ocorrer o efeito nesting caso o melhor subconjunto contenha alguma das características que foram eliminadas.

A principal vantagem desse método é o custo computacional, quando se deseja obter conjuntos grandes em relação ao total de características. Outros detalhes sobre esse método encontram-se em [Jain and Zongker, 1997,Theodoridis and Koutroumbas, 1999].

Mais l - Menos r (PTA) [Somol et al., 1999,Theodoridis and Koutroumbas, 1999]

O método mais l - menos r, cujo nome original é ``Plus $l$ - Take Away $r$'' (PTA), foi criado visando a evitar o efeito nesting. Basicamente, em cada iteração, primeiro o algoritmo adiciona $l$ elementos ao conjunto de características usando o método de seleção para frente (SFS) e, posteriormente, elimina $r$ características usando a busca seqüencial para trás (SBS). Os valores de $l$ e $r$ devem ser determinados pelo usuário. Na versão botton-up, $l$ deve ser maior que $r$. Já na versão top-down, $l < r$. Segue o algoritmo que detalha esse processo:

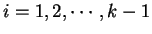
Conforme mencionado, esse método de busca evita o problema de nesting, mas com ele surge um novo problema: a determinação dos valores de $l$ e $r$. Se forem tomados valores muito pequenos, é possível que o problema nesting não seja evitado. Por outro lado, se os valores de $l$ e $r$ forem muito grandes, o algoritmo torna-se muito lento.

Algoritmos de Busca Seqüencial Generalizada (GSFS e GSBS) [Somol et al., 1999,Theodoridis and Koutroumbas, 1999]

Os algoritmos de busca seqüencial generalizada inserem (no caso do GSFS) ou removem (no caso do GSBS) tuplas (subconjuntos) de características ao invés de o fazerem com apenas uma característica por iteração. Para possibilitar o funcionamento dos algoritmos generalizados, devem-se utilizar funções que determinam a significância de tuplas.

Os dois algoritmos de busca generalizada mais conhecidos são os seguintes:

1. GSFS: essa é a versão generalizada do algoritmo SFS. Devem-se assumir que inicialmente $\calX \leftarrow \emptyset$

   
   
   

2. GSBS: essa é a versão generalizada do algoritmo SBS. Devem-se assumir que inicialmente $\calX \leftarrow \calY$
   

   
   
   

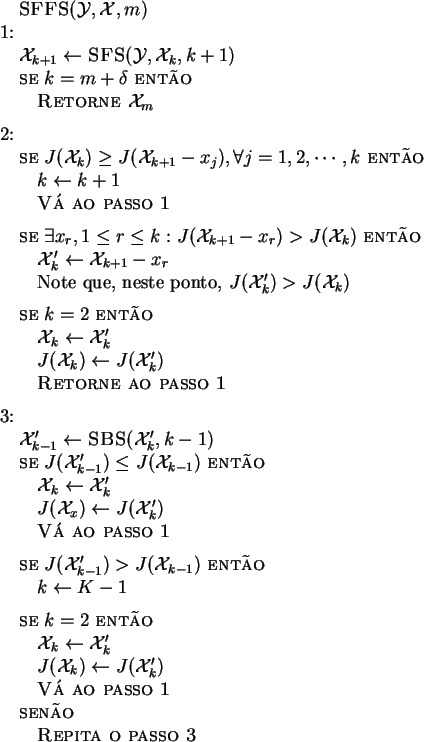
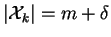
Além desses algoritmos, há também uma versão generalizada do algoritmo PTA, em que, para cada passo, ao invés de serem inseridas ou excluídas características individuais, são avaliadas tuplas de tamanho definido pelo usuário (para frente e para trás). Esse algoritmo proporciona resultados muito próximos do resultado ótimo, mas seu custo computacional pode torná-lo proibitivo em conjuntos de características grandes [Pudil et al., 1994].

Como esses algoritmos inserem ou removem tuplas de características ao invés de características individuais, a probabilidade de ocorrer o efeito nesting é reduzida. Porém, o problema da escolha do tamanho dessas tuplas ($o$) é fundamental para a obtenção do equilíbrio entre tempo de execução e qualidade dos resultados. Quando o tamanho das tuplas for muito grande, o algoritmo torna-se muito lento. Por outro lado, quando esse valor for pequeno, os resultados se aproximam das versões não generalizadas desses algoritmos.

Métodos de Busca Seqüencial Flutuante (SFSM)

Os métodos de busca seqüencial flutuante para frente e para trás, propostos em [Pudil et al., 1994] podem ser vistos como generalizações do método mais l - menos r, em que os valores de $l$ e $r$ são determinados e atualizados dinamicamente. Como os próprios nomes dizem, o método de busca para frente (SFFS) é a versão botton-up, enquanto o de busca para trás (SFBS), top-down.

O fluxograma da figura 3.14 resume o funcionamento da versão para frente desse algoritmo.

.75SFFS.eps Fluxograma simplificado do algoritmo SFFS. Adaptada de [Jain and Zongker, 1997].

A seguir, apresentamos o algoritmo em sua forma completa. Para tornar mais clara a exposição, é suposto que $k$ características já foram selecionadas do conjunto completo de características $\calY = \{y_j \vert j=1, 2, \cdots, N\}$ para formar o conjunto $\calX_k$ com a correspondente função critério $J(\calX_k)$. Porém, esse algoritmo deve iniciar-se com $k=0$ e $\calX = \emptyset$. Adicionalmente, os valores de $J(\calX_i)$ de todos os subconjuntos precedentes de tamanho $i = 1, 2, \cdots, k-1$, são conhecidos e foram armazenados.

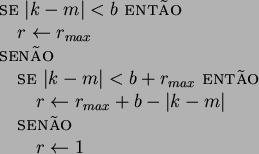
Pode-se notar que a condição de parada é que $\vert\calX_k\vert = m + \delta$, em que $\delta$ é um valor de tolerância que é utilizado para que o algoritmo não pare na primeira vez em que o conjunto $\calX_k$ tenha tamanho $m$, pois o problema de nesting só pode ser evitado se forem realizados cálculos com $\calX_{k+1}$. Normalmente utiliza-se um valor pequeno para $\delta$ (por exemplo, $\delta \leq 3$).

A versão top-down desse algoritmo (SFBS) é bastante análoga a esse, diferenciando-se somente na ordem em que os algoritmos SFS e SBS são executados e em alguns critérios de avaliação dos conjuntos. Obviamente, no SFBS, inicia-se com $k = N$.

Esses métodos proporcionam soluções muito próximas da solução ótima com um pequeno custo computacional. Segundo Jain et al. [Jain and Zongker, 1997,Jain et al., 2000], esses são os métodos que melhor combinam tempo de execução com qualidade dos resultados.

Métodos Adaptativos de Busca seqüencial flutuante [Somol et al., 1999] (ASFSM)

Os métodos adaptativos de busca seqüencial flutuante para frente e para trás (ASFFS e ASFBS) foram construídos como uma evolução dos métodos de busca seqüencial flutuante (SFSM) de forma a tornar o algoritmo generalizado, adicionando-se ou removendo-se tuplas de características, ao invés de características individuais.

Tomando-se o algoritmo SFFS como exemplo, podem-se notar que somente os passos para trás são condicionais e somente esses permitem que o conjunto de características de um determinado tamanho seja melhorado. Por outro lado, os passos para frente não podem ser condicionais, pois se eles fossem, o algoritmo poderia teoricamente cair em um ciclo infinito (repetindo a adição condicional e remoção condicional de características). Por não serem condicionais, os passos para frente podem encontrar um subconjunto que é pior que o melhor de uma certa dimensão encontrado em iterações anteriores.

Para eliminar esse problema, se o passo para frente encontrar um subconjunto que é pior que o melhor de todos encontrado em um passo anterior, deve-se descartar o subconjunto atual e considerar o melhor subconjunto como o conjunto atual. Essa troca violenta entre o conjunto atual e o melhor conjunto encontrado não proporciona um ciclo infinito, pois esse caso só ocorre quando o melhor conjunto de características foi encontrado em um passo para trás.

Os métodos ASFSM (adaptativos seqüenciais flutuantes) não são simples generalizações dos métodos SFSM, pois, além de inserirem ou excluírem tuplas de características em seus passos, o tamanho dessas tuplas também é determinado dinamicamente. São realizados testes com tuplas de vários tamanhos para determinar-se a solução, mas, para limitar o tempo de execução do algoritmo, o usuário deve definir o tamanho máximo absoluto das tuplas, $r_{max}$. Para tornar o algoritmo mais eficiente, há um mecanismo que faz com que o tamanho das tuplas seja inversamente proporcional à distância entre o tamanho do conjunto sendo avaliado no passo atual (conjunto atual) e o tamanho final $m$. Assim, quando os conjuntos sendo avaliados são muito menores ou muito maiores que $m$, o ASFM é mais rápido, pois são inseridas ou excluídas tuplas menores de características. Com isso, o algoritmo chega mais rápido a um conjunto atual de tamanho próximo de $m$ e vai aumentando a precisão da busca. Um outro parâmetro que deve ser definido pelo usuário é $b$, o qual é usado para determinar a relação entre o tamanho do conjunto atual e o tamanho máximo das tuplas. Assim, os parâmetros $b$, $r_{max}$ e $m$ são utilizados para determinar o tamanho máximo das tuplas para a busca no conjunto atual, sendo $r$ o tamanho atual da tupla. O algoritmo a seguir descreve como $r$ é calculado durante a execução do ASFSM:

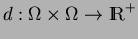
A determinação dos valores de $b$ e $r_{max}$ não é automática. Porém esses parâmetros não são tão críticos em relação à execução do método e de seus resultados quando comparados com os parâmetros $o$ (tamanho das tuplas, no caso dos algoritmos generalizados tradicionais), $l$ e $r$ (no caso do método PTA). Uma característica importante desse método é que, se $r_{max} = 1$, ele é executado exatamente da mesma maneira que os métodos SFSM, o que faz com que a desigualdade a seguir seja sempre válida:

$$J(\calX_m^{ASFM}) \geq J(\calX_m^{SFSM}),$$ (3.34)

em que $\calX_m^{ASFM}$ e $\calX_m^{SFSM}$ são, respectivamente, o subconjunto obtido com o método ASFM e o subconjunto obtido com o método SFSM. Por outro lado, o limite inferior do tempo de execução do ASFM é igual ao tempo de execução do método SFSM. Quando o valor de $b$ e $r_{max}$ são grandes e quando $N$ é grande e $m$ possui um valor próximo de $N/2$, o tempo de execução do ASFSM pode ser muito grande se comparado com SFSM . Caso contrário, o tempo de execução é menor. Maiores detalhes sobre esse método podem ser encontrados em [Somol et al., 1999].

Na seção 5.2.1 e no artigo [Campos et al., 2000c], mostramos os testes e resultados obtidos da comparação desses dois métodos para um problema de seleção de características com dados reais.

Recentemente, o grupo de pesquisa de Pudil (Academy of Sciences of the Czech Republic), criador dos métodos SFSM e ASFSM, propôs novos algoritmos de busca para seleção de características [Kittler et al., 2001]. Dentre eles, os principais métodos são os seguintes:

• Busca oscilatória [Somol and Pudil, 2000]: Esse método faz a busca sem que seja necessário definir um sentido (para frente ou para trás). A inicialização é feita com um conjunto de características de tamanho $m$, que é o tamanho do conjunto desejado. São executadas inserções e remoções de características para maximizar a função critério. Para isso, são utilizados outros métodos de busca, como os métodos seqüenciais, os flutuantes ou o método exaustivo. A escolha desses métodos depende da relação entre qualidade dos resultados e tempo de execução desejados. A busca pode ser restringida por um limite de tempo, caso o método seja aplicado a sistemas de tempo real. Os autores mostraram que, na maioria dos casos, os métodos de busca oscilatória proporcionaram resultados melhores que os outros métodos sub-ótimos existentes [Kittler et al., 2001].
• Fast Branch and Bound [Somol et al., 2000,Somol et al., 2001]: O algoritmo rápido de branch and bound baseia-se em um mecanismo de predição o qual permite que os mesmos resultados que o branch and bound sejam obtidos com um número menor de computações da função critério em nós internos da árvore. Informações sobre a contribuição individual das características são computadas durante a execução do algoritmo. A predição opera individualmente dependente de características particulares e do contexto da busca na árvore. Os experimentos dos autores [Kittler et al., 2001] mostraram que o tempo de execução desse algoritmo é menor que o de todas as outras versões do método Branch and Bound existentes.

Como esses métodos são muito recentes, eles não foram incorporados no conjunto de experimentos de seleção de características realizados no decorrer deste trabalho de mestrado.