




Next: Experimentos de Seleção de
Up: Método Proposto para Seleção
Previous: Algoritmo e complexidade
Contents
Index
Considerações Sobre o Comportamento da Função Critério
Nesta seção, serão discutidas as principais propriedades dessa abordagem, as quais nos
motivaram a utiliza-la em seleção de características. Tais propriedades se
relacionam com a distância entre os suportes (protótipos) das classes diferentes e com o
quão os conjuntos são compactos (compacidade). Cada parâmetro das equações
3.36 e 3.37 será discutido isoladamente, sendo
posteriormente analisados os resultados da integração desses parâmetros nessas
equações. Para facilitar a ilustração dos casos, os resultados a serem mencionados em relação a compacidade são válidos para conjuntos (classes de padrões)
com distribuições aproximadamente isotrópicas. As considerações a
respeito da distância entre os protótipos também são válidas para conjuntos de
padrões com distribuições normais. Posteriormente há uma discussão
considerando casos genéricos.
- Compacidade. Fixando-se a distância entre os protótipos de classes
diferentes e o raio da bola
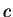 , quando a distribuição de uma classe
, quando a distribuição de uma classe
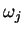 for compacta (possuir compacidade grande), para a maioria dos
padrões
for compacta (possuir compacidade grande), para a maioria dos
padrões
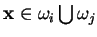 , os valores de
, os valores de
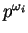 serão grandes, pois o grau de
pertinência de um padrão a sua classe é inversamente proporcional à distancia
entre esse e o protótipo dessa classe. Caso contrário (quando a compacidade
da classe for grande), os valores de
serão grandes, pois o grau de
pertinência de um padrão a sua classe é inversamente proporcional à distancia
entre esse e o protótipo dessa classe. Caso contrário (quando a compacidade
da classe for grande), os valores de
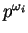 serão pequenos
para a maioria dos padrões
serão pequenos
para a maioria dos padrões
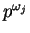 .
.
- Distância entre os protótipos. Seja
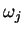 e
e 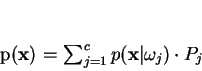 duas
classes e
duas
classes e 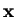 ,
, 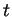 ,
, 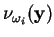 padrões com
padrões com
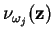 e
e
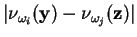 ,
,
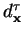 , fixando-se a compacidade da distribuição das classes de padrões e o raio da bola
, fixando-se a compacidade da distribuição das classes de padrões e o raio da bola 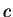 , quando a distância entre os protótipos de classes diferentes for grande, será mais provável
que um dado padrão
, quando a distância entre os protótipos de classes diferentes for grande, será mais provável
que um dado padrão 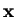 esteja próximo do protótipo de uma classe e distante de
outra. Sendo
esteja próximo do protótipo de uma classe e distante de
outra. Sendo 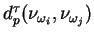 o protótipo que se encontra mais próximo do
padrão
o protótipo que se encontra mais próximo do
padrão 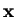 e
e 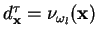 o protótipo que se encontra mais distante do
padrão
o protótipo que se encontra mais distante do
padrão 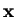 , o valor de
, o valor de
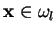 será grande, e o valor de
será grande, e o valor de
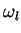 será pequeno (para
será pequeno (para
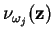 e
e
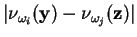 ). Com isso, a diferença
). Com isso, a diferença
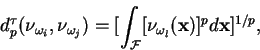 será grande. Se isso ocorrer na
maioria dos padrões dentro da bola
será grande. Se isso ocorrer na
maioria dos padrões dentro da bola
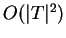 , o valor de
, o valor de
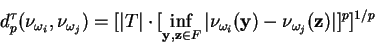 será grande. Como isso provavelmente ocorrerá para a maioria dos padrões, o valor total da distância
será grande. Como isso provavelmente ocorrerá para a maioria dos padrões, o valor total da distância
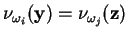 será grande.
Caso a distância entre os protótipos de classes diferentes seja pequena, seguindo o mesmo racionício, conclui-se que o valor de
será grande.
Caso a distância entre os protótipos de classes diferentes seja pequena, seguindo o mesmo racionício, conclui-se que o valor de
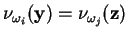 será pequeno.
será pequeno.
- Tamanho da bola. Fixando-se a distância entre os protótipos e a
compacidade, devemos considerar dois casos:
- Quando for utilizada uma bola muito pequena, para todos os
padrões
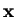 , a bola
, a bola
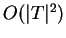 irá conter somente os padrões
da classe de
irá conter somente os padrões
da classe de 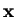 . Nesse caso, a seguinte igualdade será válida:
. Nesse caso, a seguinte igualdade será válida:
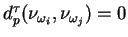 (para
(para
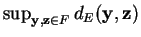 ,
, 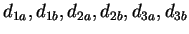 podendo ser
podendo ser 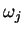 ou
ou 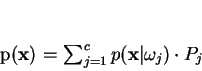 ). Com isso,
). Com isso,
![\begin{displaymath}
d_p^{\tau} (\nu_{\omega_i}, \nu_{\omega_j}) =
[\int_{\calF}[\nu_{\omega_l}({\bf x})]^p d{\bf x}]^{1/p},
\end{displaymath}](img351.png) |
(3.38) |
o que significa que o valor de
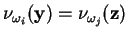 será exclusivamente dependente da compacidade das classes.
será exclusivamente dependente da compacidade das classes.
- Quando for utilizada uma bola muito grande, para qualquer padrão
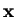 ,
,
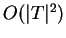 conterá todos os padrões de treinamento do espaço de características. Com isso, pode-se mostrar que a seguinte igualdade se torna válida:
conterá todos os padrões de treinamento do espaço de características. Com isso, pode-se mostrar que a seguinte igualdade se torna válida:
![\begin{displaymath}
d_p^{\tau} (\nu_{\omega_i}, \nu_{\omega_j}) = [\vert T\vert ...
...u_{\omega_i}({\bf y}) - \nu_{\omega_j}({\bf z})\vert]^p]^{1/p}
\end{displaymath}](img352.png) |
(3.39) |
Como resultado, a importância da compacidade e da distância entre os
protótipos é reduzida, pois o valor da métrica dependerá exclusivamente da mínima
diferença global entre o grau de pertinência de dois padrões de classes
diferentes. Assim, não importando a distribuição dos padrões no espaço de
características, se existirem dois padrões 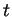 e
e 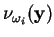 tais que
tais que
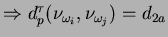 , então teremos em
, então teremos em
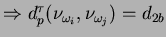 .
.
Por isso, a determinação do valor de 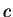 é muito importante na utilização
da distância de [Lowen and Peeters, 1998] como função critério. Para determinar o
melhor valor de
é muito importante na utilização
da distância de [Lowen and Peeters, 1998] como função critério. Para determinar o
melhor valor de 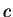 para um dado conjunto de padrões de treinamento,
uma estratégia possível é a de tentativa e erro com vários valores diferentes
de
para um dado conjunto de padrões de treinamento,
uma estratégia possível é a de tentativa e erro com vários valores diferentes
de 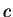 , sendo que o valor máximo deve ser menor que
, sendo que o valor máximo deve ser menor que
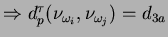 . Na seção 5.3, estão descritos experimentos de seleção de características com variação no tamanho da bola.
. Na seção 5.3, estão descritos experimentos de seleção de características com variação no tamanho da bola.
Considerando a utilização de uma bola cujo tamanho seja ideal para avaliar um
determinado conjunto de características com um certo conjunto de treinamento
de duas classes, podemos construir uma lista de possibilidades, denotando por
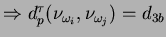 seus prováveis resultados. A
relação entre os resultados será comentada posteriormente.
seus prováveis resultados. A
relação entre os resultados será comentada posteriormente.
- Ambas as classes são compactas e...
- a distância entre os protótipos é pequena
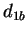
- a distância entre os protótipos é grande
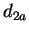
- Ambas as classes são esparsas e...
- a distância entre os protótipos é pequena
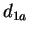
- a distância entre os protótipos é grande
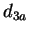
- Uma classe possui compacidade grande e a outra possui compacidade pequena e...
- a distância entre os protótipos é pequena
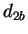
- a distância entre os protótipos é grande
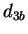
.6possibilidades.eps
Exemplos de distribuições de duas classes em um espaço de
características com dimensão 2. Cada círculo representa a compacidade de uma
classe e os pontos representam protótipos.
A figura 3.15 ilustra esses casos. Considerando que as duas
classes possuem distribuições aproximadamente isotrópicas e que a bola
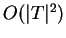 possui tamanho ideal. Podemos afirmar que, intuitivamente,
é mais provável que a distância
possui tamanho ideal. Podemos afirmar que, intuitivamente,
é mais provável que a distância 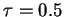 será maior que todas as outras. Da
mesma forma, podemos dizer que as distâncias
será maior que todas as outras. Da
mesma forma, podemos dizer que as distâncias 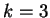 e
e 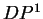 provavelmente serão as maiores distâncias e que a distância
provavelmente serão as maiores distâncias e que a distância 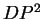 provavelmente será menor que
provavelmente será menor que 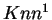 que, por sua vez, provavelmente será
menor que
que, por sua vez, provavelmente será
menor que 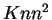 .
.
Essas estimativas resultam da análise dos casos considerando as propriedades citadas anteriormente.
Caso as distribuições dos conjuntos (classes de padrões) com distribuições não normais, convexas ou com formas mais ``complicadas'',
torna-se mais difícil realizar uma estimativa dos resultados dessa função critério. Porém
pode-se dizer que a influência do número de padrões de classes diferentes
que a bola
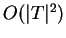 engloba, para diferentes
engloba, para diferentes 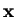 , tem mais
importância que a distância entre os protótipos. A bola
, tem mais
importância que a distância entre os protótipos. A bola
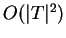 serve como uma medida de sobreposição das distribuições das classes no espaço de características. Se duas classes estiverem muito sobrepostas, o valor da função critério será pequeno. A seguir, mostramos resultados que ilustram esse fato.
serve como uma medida de sobreposição das distribuições das classes no espaço de características. Se duas classes estiverem muito sobrepostas, o valor da função critério será pequeno. A seguir, mostramos resultados que ilustram esse fato.





Next: Experimentos de Seleção de
Up: Método Proposto para Seleção
Previous: Algoritmo e complexidade
Contents
Index
Teofilo Emidio de Campos
2001-08-29
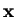 , a bola
, a bola
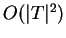 irá conter somente os padrões
da classe de
irá conter somente os padrões
da classe de 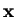 . Nesse caso, a seguinte igualdade será válida:
. Nesse caso, a seguinte igualdade será válida:
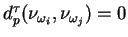 (para
(para
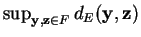 ,
, 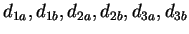 podendo ser
podendo ser 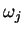 ou
ou 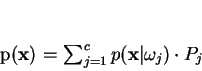 ). Com isso,
). Com isso,
![\begin{displaymath}
d_p^{\tau} (\nu_{\omega_i}, \nu_{\omega_j}) =
[\int_{\calF}[\nu_{\omega_l}({\bf x})]^p d{\bf x}]^{1/p},
\end{displaymath}](img351.png)
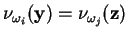 será exclusivamente dependente da compacidade das classes.
será exclusivamente dependente da compacidade das classes.
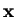 ,
,
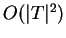 conterá todos os padrões de treinamento do espaço de características. Com isso, pode-se mostrar que a seguinte igualdade se torna válida:
conterá todos os padrões de treinamento do espaço de características. Com isso, pode-se mostrar que a seguinte igualdade se torna válida:
![\begin{displaymath}
d_p^{\tau} (\nu_{\omega_i}, \nu_{\omega_j}) = [\vert T\vert ...
...u_{\omega_i}({\bf y}) - \nu_{\omega_j}({\bf z})\vert]^p]^{1/p}
\end{displaymath}](img352.png)
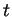 e
e 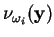 tais que
tais que
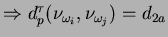 , então teremos em
, então teremos em
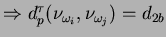 .
.