


Vários métodos de segmentação não supervisionada de imagens usando grafos, consideram um grafo esparso G(V, E), onde os vértices no conjunto V são os pixels e as arestas em E são definidas entre pixels vizinhos. Os pesos das arestas são dados por uma função de dissimilaridade entre as características dos pixels vizinhos (ex: magnitude do gradiente de intensidades), ou pela sua noção dual dada por uma função de afinidade/similaridade.
Uma partição do conjunto finito V é um conjunto P de subconjuntos disjuntos e não vazios de V, cuja união é V (isto é, ∀X,Y ∈ P, X ∩ Y = ∅ se X ≠ Y e ∪{X ∈ P} = V). Qualquer elemento de uma partição P de V é chamada de região de P. Se x é um elemento de V, existe uma única região de P que contém x; essa única região é denotada por [P]x. Dadas duas partições P e P' de um conjunto V, dizemos que P' é um refinamento de P se qualquer região de P' está incluída em uma região de P. Uma hierarquia (em V) é uma sequência H = (P0, ..., Pℓ) de partições de V tal que Pi-1 é um refinamento de Pi, para qualquer i ∈ {1, ..., ℓ}. Se H = (P0, ..., Pℓ) é uma hierarquia, o inteiro ℓ é chamado a profundidade de H. Uma hierarquia H = (P0, ..., Pℓ) é chamada de completa se Pℓ = {V} e se P0 contém todos os elementos individuais de V como regiões separadas (isto é, P0 = {{x} | x ∈ V}).
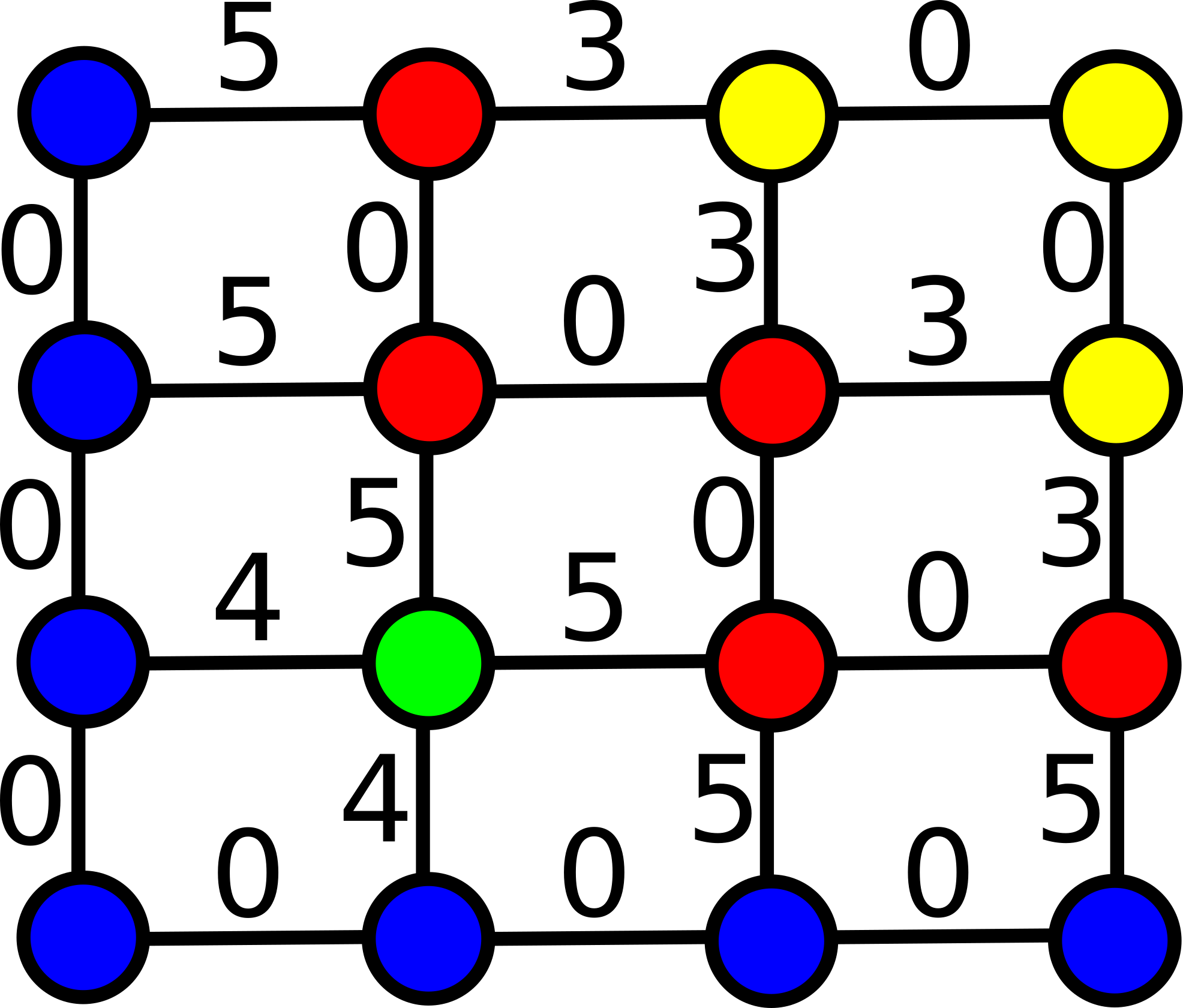
Para um dado grafo derivado da imagem, uma relação binária entre pixels contida no produto cartesiano V \times V que satisfaz as propriedades de reflexividade, simetria e transitividade, induz naturalmente uma segmentação da imagem, pois uma relação de equivalência permite particionar o grafo em classes de equivalência. Por exemplo, para um grafo não direcionado, considere a relação binária a \overset{\kappa}{\leadsto} b tal que existe um caminho interligando os pixels a e b, contendo apenas arestas com pesos abaixo de um dado limiar \kappa (isto é, ∃ um caminho \pi_{a \leadsto b} = \langle p_1, \ldots, p_n\rangle com a = p_1 e b = p_n, tal que \omega(p_i, p_{i+1}) < \kappa, para qualquer i \in \{1, \ldots, n-1\}).
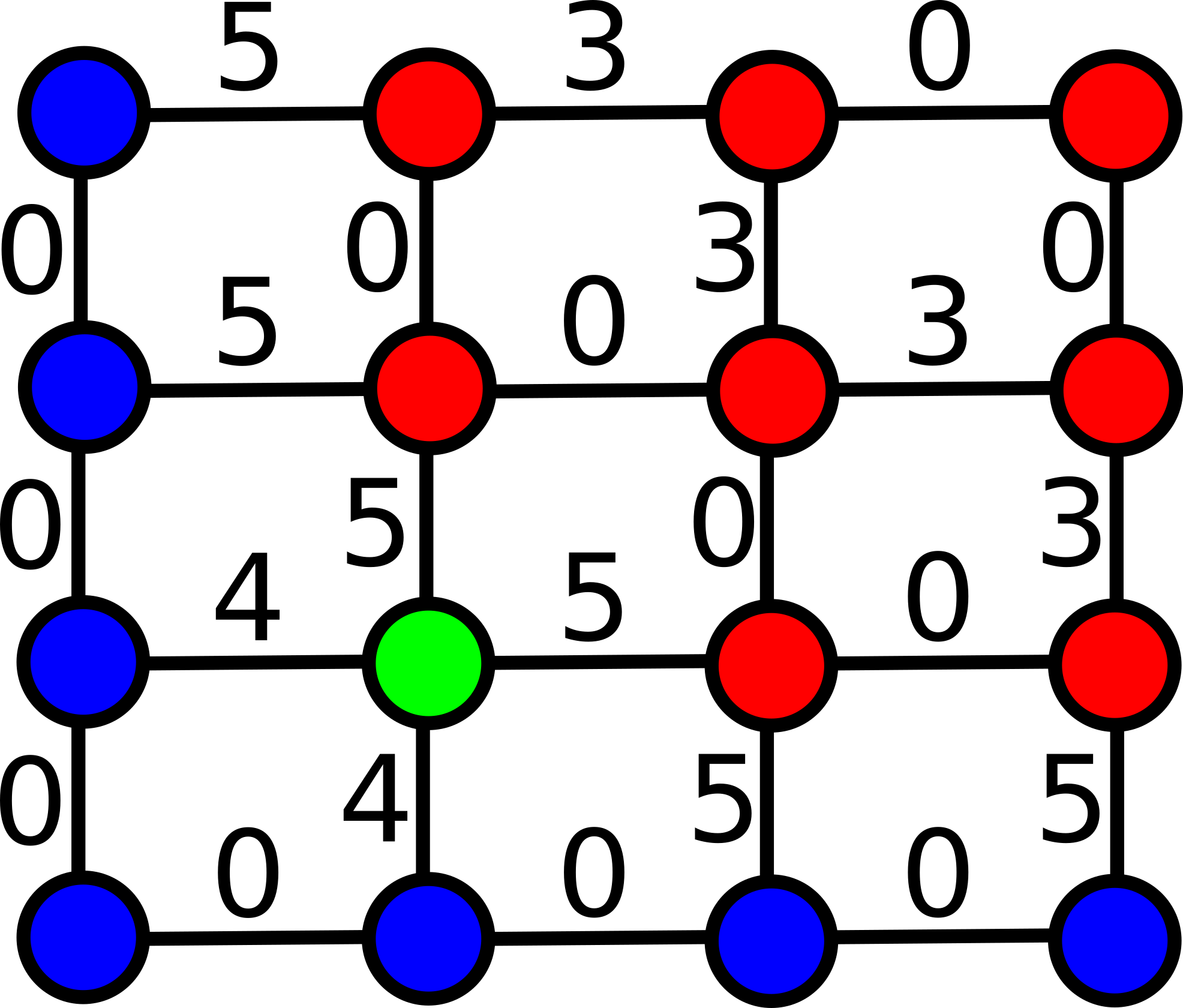
As partições geradas por essa relação binária correspondem aos componentes conexos do grafo, após a remoção de todas as arestas com pesos maiores ou iguais à \kappa. Variando o parâmetro \kappa, é possível construir uma hierarquia das partições. Veja o exemplo abaixo:
 |
 |
 |
| (a) Grafo de imagem com vizinhança-4 | (b) Partições para κ=3 | (c) Partições para κ=4 |
 |
 |
|
| (d) Partições para κ=5 | (e) Partições para κ=6 |
Esse procedimento para a criação de hierarquias tal como descrito acima é conhecido como hierarquia de zona quase plana (quasi-flat zone hierarchy [1]).
Dado um grafo G(V, E), uma partição de V é conexa (em G) se todas as suas regiões são conexas e uma hierarquia em V é conexa (em G) se todas as suas partições são conexas. Uma hierarquia conexa pode ser tratada de forma equivalente por meio de um grafo ponderado nas arestas, com w : E(G) → ℝ sendo a função de peso, tal como explicado na próxima seção.
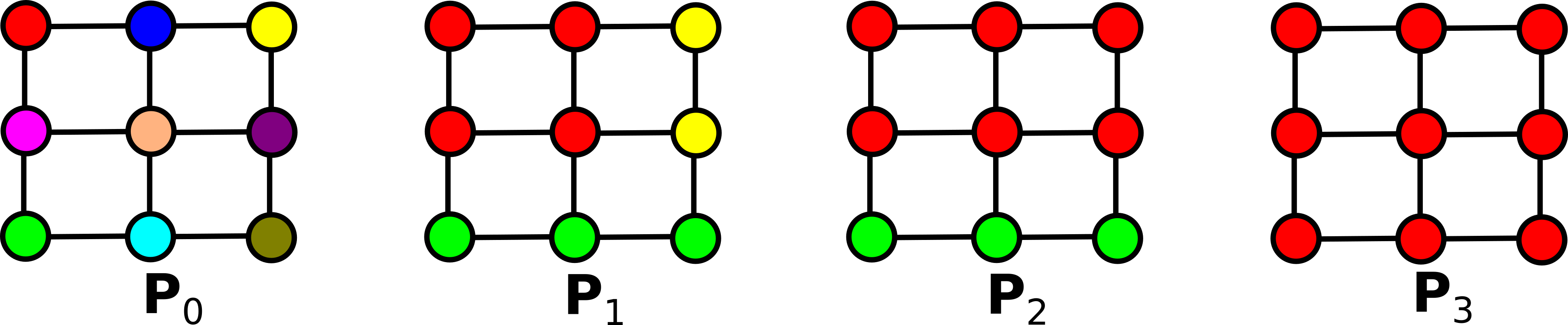
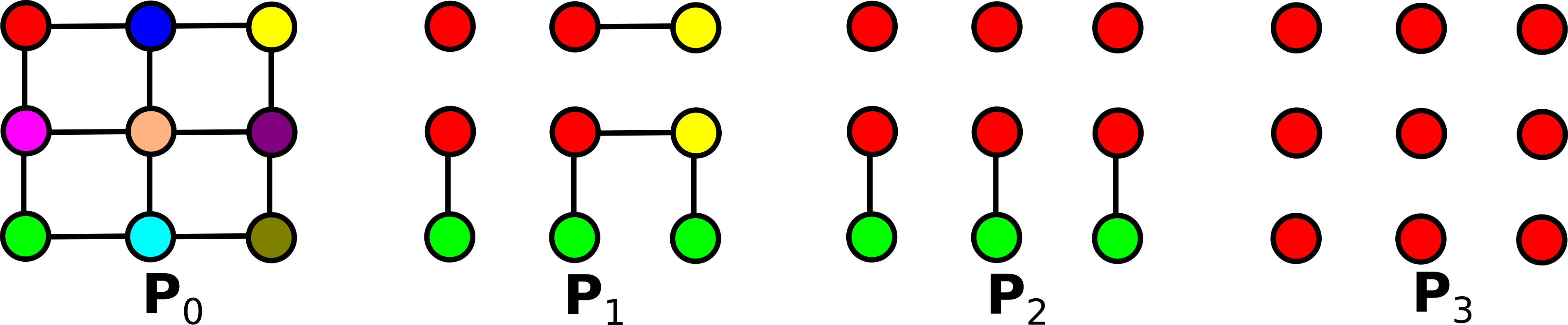
Seja P uma partição de V, o corte de P (em G), denotado por ϕG(P), é o conjunto de arestas de G formadas por dois vértices em regiões diferentes de P, isto é, ϕG(P) = {{x, y} ∈ E | [P]x ≠ [P]y }.
Seja H = (P0, ..., Pℓ) uma hierarquia em V. O mapa de saliência de H é o mapa ΦG(H) de E a {0, ..., ℓ} de modo que o peso de qualquer aresta u para ΦG(H) é o máximo valor λ para o qual u pertence ao corte de Pλ:
ΦG(H)(u) = max{λ ∈ {0, ..., ℓ}| u ∈ ϕG(Pλ)}
Por exemplo, considere o exemplo abaixo de uma hierarquia conexa H = (P0, ..., Pℓ) com ℓ=3 em um grafo de vizinhança-4:
 |
 |
 |
[1] Hierarchical Segmentations with Graphs: Quasi-flat Zones, Minimum Spanning Trees, and Saliency Maps.
Jean Cousty, Laurent Najman, Yukiko Kenmochi, Silvio Guimarães.
Journal of Mathematical Imaging and Vision, volume 60, pages 479-502 (2018)
| Max-tree com atributo de altura |
Valores de extinção nas folhas |
| Max-tree com área dos vértices |
Max-tree com atributo de área (acumulada) |
Valores de extinção nas folhas |
| Max-tree com volume dos vértices |
Max-tree com atributo de volume (acumulado) |
Valores de extinção nas folhas |
Artigos relacionados:
A cada iteração t, os conjuntos S_t e M_t são informados e uma IFT é calculada de forma diferencial/incremental em relação a floresta da iteração anterior t-1. As árvores com pixels em M_t serão removidas e suas regiões disponibilizadas para a nova conquista por parte das raízes restantes e das novas sementes em S_t. Essas raízes são representadas por pixels das árvores não removidas que são adjacentes a pixels das árvores removidas. Estes pixels são denotados pixels de fronteira.
Artigos relacionados:
Exemplo em filtragem: Para uma dada imagem binária I com ruído e imperfeições, desejamos obter uma imagem filtrada F. Considere a imagem I abaixo.

Os ruídos e imperfeições finas da imagem I resultam em uma elevada quantidade de pixels de borda. Logo, a fim de eliminar os ruídos devemos reduzir o número de transições preto/branco na imagem filtrada F. Isso pode ser formulado pela seguinte energia:
E = \sum_{(a,b)\in E} \lvert F(a) - F(b) \rvert.
A minimização da energia acima possui como soluções triviais imagens filtradas F de brilho constante. Portanto, devemos incluir um segundo termo que penaliza resultados divergentes em relação à imagem I:
E = \kappa \sum_{(a,b)\in E} \lvert F(a) - F(b) \rvert + \lambda \sum_{a \in {\cal D}_I} \lvert I(a) - F(a) \rvert.
A energia acima pode ser minimizada através do algoritmo do fluxo máximo/corte mínimo, utilizando o seguinte grafo no qual:
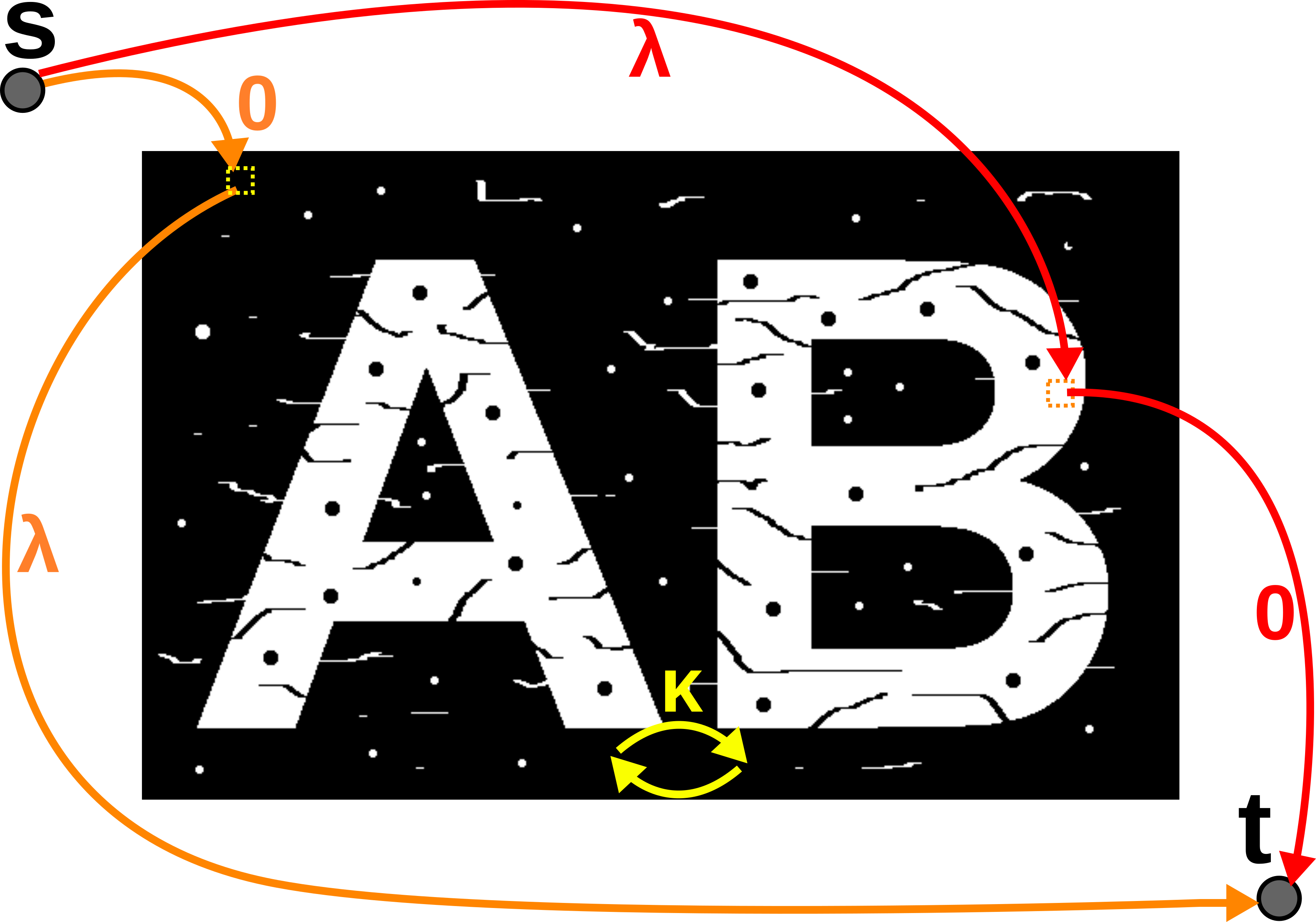
Variando os pesos \kappa e \lambda dos termos da energia temos diferentes soluções:
 |
 |
 |
 |
| \kappa=1 e \lambda=1 | \kappa=2 e \lambda=1 | \kappa=3 e \lambda=1 | \kappa=5 e \lambda=1 |
Observe que a imagem filtrada resultante não pode ser obtida via filtragem conexa.
Artigo: Oriented Image Foresting Transform Segmentation by Seed Competition
Artigo: Image Segmentation by Oriented Image Foresting Transform: Handling Ties and Colored Images
Artigo: Geodesic Star Convexity for Interactive Image Segmentation
Artigo: Image Segmentation by Oriented Image Foresting Transform with Geodesic Star Convexity
Monografia: Segmentação de imagens utilizando passeios aleatórios em grafos
Artigo: Random Walks for Image Segmentation
Artigo: Relaxed image foresting transforms for interactive volume image segmentation
Numerando os vértices do grafo podemos representá-lo pela sua matriz de afinidade \mathbf{A}.
\mathbf{A} =
\begin{bmatrix}
w_{11} & w_{12} & w_{13} & \dots & w_{1n} \\
w_{21} & w_{22} & w_{23} & \dots & w_{2n} \\
\hdotsfor{5} \\
w_{n1} & w_{n2} & w_{n3} & \dots & w_{nn}
\end{bmatrix} =
\begin{bmatrix}
0 & 2 & 0 & 2 & 0.1 & 0 & 0 & 0 & 0 \\
2 & 0 & 5 & 3 & 0 & 0 & 0 & 0 & 0 \\
0 & 5 & 0 & 2 & 0 & 0 & 0 & 0 & 0 \\
2 & 3 & 2 & 0 & 0 & 0 & 0 & 0 & 0.1 \\
0.1 & 0 & 0 & 0 & 0 & 1 & 3 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 0 & 4 & 2 & 0 \\
0 & 0 & 0 & 0 & 3 & 4 & 0 & 2 & 4 \\
0 & 0 & 0 & 0 & 0 & 2 & 2 & 0 & 1 \\
0 & 0 & 0 & 0.1 & 1 & 0 & 4 & 1 & 0
\end{bmatrix} =
Considere o problema de dividir o grafo em grupos de vértices de alta afinidade. Um grupo pode ser especificado por um vetor \mathbf{u} = [u_1 \ldots u_n]^T, no qual u_i representa o grau de pertinência do i-ésimo vértice ao conjunto.
Gostaríamos de maximizar o seguinte funcional de energia:
E(\mathbf{u}) = \mathbf{u}^T \mathbf{A} \mathbf{u} = \sum_i \sum_j u_i w_{ij} u_j
sob a restrição: \mathbf{u}^T \cdot \mathbf{u} = 1 \Rightarrow ||\mathbf{u}|| = 1
Dado que a matriz de afinidade é simétrica (w_{ij} = w_{ji}), ela admite uma base ortonormal (\mathbf{u_1}, \ldots , \mathbf{u_n}) de autovetores.
Logo, podemos reescrever \mathbf{u} na base de autovetores de \mathbf{A}:
\mathbf{u} = \sum_i c_i \mathbf{u_i}
Substituindo na equação, temos:
\mathbf{u}^T \mathbf{A} \mathbf{u} = (\sum_j c_j \mathbf{u_j})^T \mathbf{A} (\sum_i c_i \mathbf{u_i})
= (\sum_j c_j \mathbf{u_j}^T)(\sum_i c_i \mathbf{A} \mathbf{u_i})
= (\sum_j c_j \mathbf{u_j}^T)(\sum_i c_i \lambda_i \mathbf{u_i})
= \sum_j \sum_i (c_j c_i \lambda_i \mathbf{u_j}^T \mathbf{u_i})
Note que:
i \neq j \Rightarrow \mathbf{u_j}^T \cdot \mathbf{u_i} = 0
i = j \Rightarrow \mathbf{u_j}^T \cdot \mathbf{u_i} = 1.
Portanto temos:
\sum_j \sum_i (c_j c_i \lambda_i \mathbf{u_j}^T \mathbf{u_i}) = \sum_i (c_i^2 \lambda_i)
Note que a restrição ||\mathbf{u}|| = 1 pode ser reescrita como \sum c_i^2 = 1
Portanto, a energia corresponde a uma média ponderada dos autovalores da matriz de afinidade, com pesos c_i^2.
Dado que os autovalores são números reais, temos que o máximo valor da energia
é obtido atribuindo-se peso total para o maior autovalor. Logo, a solução
corresponde ao autovetor associado ao maior autovalor.
Artigo: Normalized Cuts and Image Segmentation
Artigo: What Energy Functions Can Be Minimized via Graph Cuts?
Artigo: Globally Optimal Segmentation of Multi-Region Objects
Artigo: Multi-Object Segmentation by Hierarchical Layered Oriented Image Foresting Transform
Artigo: Image Segmentation with Minimum Mean Cut
Artigo: Image segmentation with ratio cut