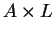 |
(3.10) |
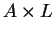 |
(3.10) |
Apesar de serem usados apenas ![]() descritores para obter cada componente de
descritores para obter cada componente de
![]() ,
, ![]() ainda varia de 0 a
ainda varia de 0 a ![]() . Isto é, a aproximação do sinal possui o mesmo tamanho que o sinal original.
Os primeiros coeficientes de Fourier referem-se às freqüências mais baixas do
sinal, que geralmente contêm informações mais globais dos padões comumente encontrados em problemas de visão. Já os últimos
referem-se às freqüências mais altas do sinal, as quais são geralmente
associadas a informações mais
detalhadas ou finas dos padrões ou são causadas por ruídos [Gonzalez and Woods, 1992].
. Isto é, a aproximação do sinal possui o mesmo tamanho que o sinal original.
Os primeiros coeficientes de Fourier referem-se às freqüências mais baixas do
sinal, que geralmente contêm informações mais globais dos padões comumente encontrados em problemas de visão. Já os últimos
referem-se às freqüências mais altas do sinal, as quais são geralmente
associadas a informações mais
detalhadas ou finas dos padrões ou são causadas por ruídos [Gonzalez and Woods, 1992].
Por isso, pode-se reduzir a dimensionalidade desses padrões (imagens)
utilizando apenas seus ![]() primeiros descritores de Fourier. Assim, as imagens
reconstruídas a partir desses descritores apresentam borramentos e redução dos
detalhes das bordas, mas as informações mais importantes para caracterizar os
objetos contidos nas imagens não são perdidas. Portanto, pode-se efetuar
reconhecimento de objetos em imagens utilizando-se padrões
primeiros descritores de Fourier. Assim, as imagens
reconstruídas a partir desses descritores apresentam borramentos e redução dos
detalhes das bordas, mas as informações mais importantes para caracterizar os
objetos contidos nas imagens não são perdidas. Portanto, pode-se efetuar
reconhecimento de objetos em imagens utilizando-se padrões ![]() -dimensionais,
constituidos pelos
-dimensionais,
constituidos pelos ![]() primeiros descritores de Fourier das imagens. Dessa forma,
para efetuar classificação utilizando padrões com dimensionalidade menor,
pode-se representá-los por
primeiros descritores de Fourier das imagens. Dessa forma,
para efetuar classificação utilizando padrões com dimensionalidade menor,
pode-se representá-los por ![]() , tal que:
, tal que:
| (3.11) |
Na figura 3.1, há um exemplo que ilustra os efeitos da redução
da dimensionalidade na reconstrução de um sinal. Foram criados dois sinais
aleatórios discretos de tamanho 50 (![]() e
e ![]() ). Posteriormente, foi
calculada a transformada de Fourier desses sinais e, com apenas os 25
primeiros coeficientes, foi realizada a reconstrução desses sinais. Pode-se
notar que os sinais reconstruídos são uma versão ``suavizada'' dos sinais
originais. Também é possível verificar que, apesar de terem sido utilizados, no processo
de reconstrução,
metade dos descritores de Fourier disponíveis, os sinais reconstruídos
preservaram informações importantes dos originais. Dessa forma, com 25
coeficientes é visualmente possível
distingüir qual reconstrução se refere ao sinal
). Posteriormente, foi
calculada a transformada de Fourier desses sinais e, com apenas os 25
primeiros coeficientes, foi realizada a reconstrução desses sinais. Pode-se
notar que os sinais reconstruídos são uma versão ``suavizada'' dos sinais
originais. Também é possível verificar que, apesar de terem sido utilizados, no processo
de reconstrução,
metade dos descritores de Fourier disponíveis, os sinais reconstruídos
preservaram informações importantes dos originais. Dessa forma, com 25
coeficientes é visualmente possível
distingüir qual reconstrução se refere ao sinal ![]() e qual se refere ao
sinal
e qual se refere ao
sinal ![]() . Com isso, fica ilustrado como é possível efetuar uma classificação de
padrões de dimensionalidade reduzida através da transformada de Fourier.
. Com isso, fica ilustrado como é possível efetuar uma classificação de
padrões de dimensionalidade reduzida através da transformada de Fourier.
Pelas propriedades da transformada de Fourier, podemos notar que a utilização de descritores de Fourier é uma abordagem bastante eficiente de reconhecimento de padrões e visão computacional. Além disso, essa abordagem proporciona redução de dimensionalidade de forma eficiente e sem perda de informações relevantes em visão computacional.